UNIQUE SOLUTION NO SOLUTION INFINITE SOLUTIONS

A set of linear equations with the same two variables is called a system of linear equations.

The system of linear equations can have the following solutions.

(i) Unique solutions

(ii)  No solution

(iii) Infinitely many solution

Unique solution :

Intersecting lines will have one solution (or) unique solution.

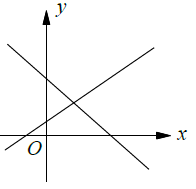
The point of intersection is known as solution.

No solution :

The parallel lines will never meet. So, there is no point of intersection that is no solution.

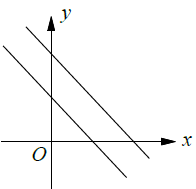
Parallel lines will have the same slope but different y-intercepts.

Infinitely many solution :

Two lines that lie exactly on top of each other or we can say that one line is exactly lying on top of another line are called coincident lines.

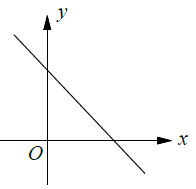
Coincident lines will have the same slope and same y-intercepts.

Problem 1 :

ax + 4y = 14

5x + 7y = 8

In the system of equations above, a is a constant and x and y are variables. If the system has no solution, what is the value of a ?

(a)  20/7    (b)  -35/4     (c)  35/4     (d) - 20/7

Solution :

ax + 4y = 14 ---(1)

5x + 7y = 8 ---(2)

By equating the slopes, we get

-a/4 = -5/7

a = (5⋅4)/7

a = 20/7

Problem 2 :

x/(y + 2) = 2

3(y - 5) - x = -16

If (x, y) is the solution to the system of equations above, what is the value of x ?

Solution :

x/(y + 2) = 2 -----(1)

3(y - 5) - x = -16 -----(2)

From (1)

x = 2(y + 2)

x = 2y + 4 -----(3)

From (2)

3y - 15 - x = -16

3y + 16 - 15 = x

x = 3y + 1-----(4)

3(3) - 2(4)

3x - 2x = 3(2y + 4) - 2(3y + 1)

x = 6y + 12 - 6y - 2

x = 10

Problem 3 :

-2x - y = -9

5x - 2y = 18

Which of the following ordered pairs (x, y) fulfills the system of equations above ?

(a) (-4, 1)      (b)  (3, 3)     (c) (2, 5)   (d)  (4, 1)

Solution :

-2x - y = -9 -----(1)

5x - 2y = 18 -----(2)

Multiply the first equation by 2 and subtract it with second equation.

2(1) - (2)

-4x - 2y - (5x - 2y) = -18 - 18 

-4x - 2y - 5x + 2y = -36

-9x = -36

Divide by -9 on both sides.

x = -36/(-9)

x = 4

By applying the value of x in (1), we get

-2(4) - y = -9

-8 - y = -9

y = -8 + 9

y = 1

So, the solution is (4, 1).

Problem 4 :

-3x + 2y = 5

-9x + 6y = 18

The system of equations above has how many solutions (x, y)

(a) Zero      (b)  Two     (c) One   (d) More than two

Solution :

-3x + 2y = 5 -----(1)

-9x + 6y = 18 -----(2)

Slopes are same, but it has different y-intercepts. Then both lines are parallel and it has no solution.

So, the answer is zero solution.

Problem 5 :

For what value of c will the system of equations below have no solution ?

cx - 2y = 6

3x + 4y = 4

Solution :

cx - 2y = 6

3x + 4y = 4

Since the system has no solution, the lines must be parallel. Then the slopes will be equal and y-intercepts will not be equal.

m₁ = m₂

c/2 = -3/4

c = (-3/4) (2)

c = -3/2

So, the value of c is -3/2.

Problem 6 :

For what value of b will the system of equations below have infinitely many solutions ?

-2x + y = 4

5x - by = -10

Solution :

-2x + y = 4 -----(1)

5x - by = -10 -------(2)

Since the system has infinitely many solution, the lines will be co-incident and they have same slope and same y-intercepts.

m₁ = m₂

2 = 5/b

b = 5/2

So, the value of b is 5/2.