UNION AND INTERSECTION OF SETS

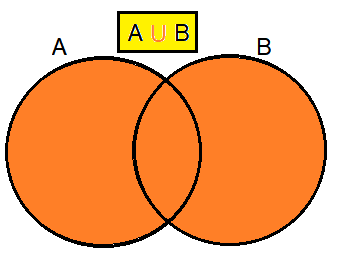
Union of two sets :

The union of two sets contains all the elements contained in either set (or both sets).

The union is notated A ⋃ B.

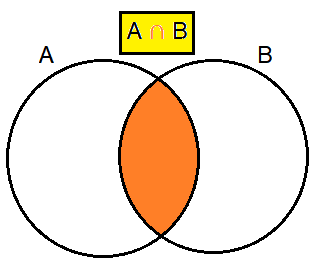
Intersection of two sets :

The intersection of two sets contains only the elements that are in both sets.

The intersection is notated A ⋂ B.

Problem 1 :

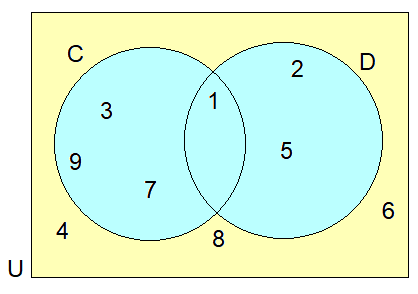
List :

Solution :

i) Set C

The elements in set C = {1, 3, 7, 9}

ii) Set D

The elements in set D = {1, 2, 5}

iii) Set U

The universal set with all the elements in set

U = {1, 2, 3, 4, 5, 6, 7, 8, 9}

iv) Set C ∩ D

The common elements in set C and D is

C ∩ D = {1}

v) Set C U D

All the elements in sets C and D is

C U D = {1, 2, 3, 5, 7, 9}

Problem 2 :

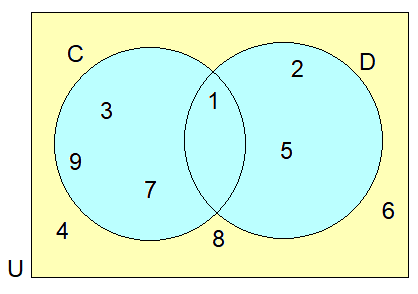
List :

Solution :

(i)  n(C)

The number of elements in set C is 4.

So, n(C) = 4

(ii)  n(D)

The number of elements in set D is 3.

So, n(D) = 3

(iii)  n(U)

The number of elements in universal set U is 9.

n(U) = 9

(iv)  n(C ∩ D)

The number of common elements in sets C and D is 1.

n(C ∩ D) = 1

(v)  n(C U D)

The number of all elements in sets C and D is 6.

n(C U D) = 6

Problem 3 :

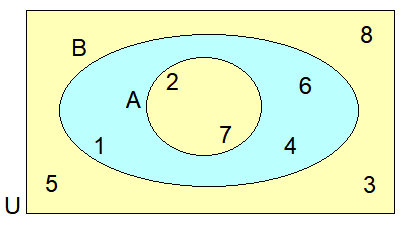
List :

Solution :

(i)  A = {2, 7}

(ii)  B = {1, 4, 6, 2, 7}

(iii)  U = {1, 2, 3, 4, 5, 6, 7, 8}

(iv)  A ∩ B = {2, 7}

(v)  A U B = {1, 2, 4, 6, 7}

Problem 4 :

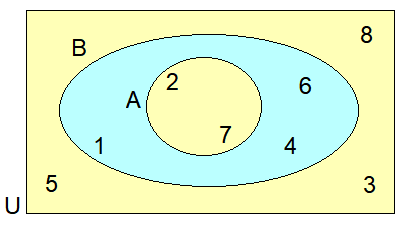
Find :

Solution :

(i)  n(A)

The number of elements in set A is 2.

So, n(A) = 2

(ii)  n(B)

The number of elements in set B is 5.

So, n(B) = 5

(iii)  n(U)

The number of elements in universal set U is 8.

n(U) = 8

(iv)  n(A ∩ B)

The number of common elements in sets A and B is 2.

n(A ∩ B) = 2

(v)  n(A U B)

The number of all elements in sets A and B is 5.

n(A U D) = 5

Problem 5 :

Consider U = {x│x ≤ 12, x € Z⁺},

A = {2, 7, 9, 10, 11} and B = {1, 2, 9, 11, 12}.

a)  Show these sets on a Venn diagram.

b)  List the elements of :

(i)  A ∩ B

(ii)  A U B

(iii)  B’

c)  Find   :

Solution :

a)

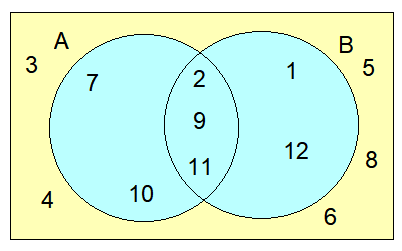
b)

(i)  A ∩B = {2, 9, 11}

(ii)  A U B = {1, 2, 7, 9, 10, 11, 12}

(iii) B’

The elements which do not belong to set B is

B’ = {3, 4, 5, 6, 7, 8, 10}

c)

(i)  n(A) = 5

(ii)  The number of elements which do not belong to set B is B’ = 7

(iii)  n(A ∩ B) = 3

(iv)  n(A U B) = 7