UNION AND INTERSECTION OF INTERVALS

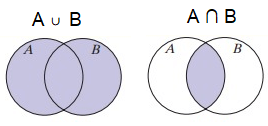
The union of sets A and B, denoted A ∪ B, is the set of elements that belong to set A or to set B or to both sets A and B.

The intersection of two sets A and B, denoted A ∩ B, is the set of elements common to both A and B.

A union B The elements in A or B or both

A intersection B The elements in A and B

Find the union or intersection as indicated. Find the intersection and union of sets as indicated. Write the answers in interval notation.

Problem 1 :

(-∞, 1/2) ∩ [-3, 4)

To find the intersection, graph each interval separately. Then find the real numbers common to both intervals.

By observing he first two number lines, between -3 to 1/2 is in common. So,

the intersection is [-3, 1/2).

Problem 2 :

(-∞, -2) ∪ [-4, 3)

Solution :

To find the union, graph each interval separately. The union is the collection of real numbers that lie in the first interval, the second interval, or both intervals.

The union is (-∞, 3).

Problem 3 :

(-2, 5) ∩ [-1, ∞)

Solution :

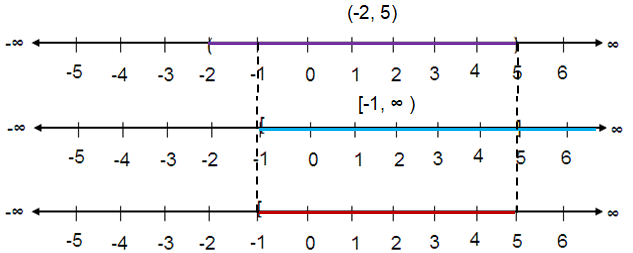
The intersection is [-1, 5).

Problem 4 :

(-2, 5) ∪ [-1, ∞)

Solution :

To find the solution for (-2, 5), we have to shade between -2 and 5 in which -2 and 5 are excluded.

To find the solution for [-1, ∞), we have to shade between -1 and ∞.

So, union of these two sets will contain the values from -2 to ∞.

The union is (-2, ∞).

Problem 5 :

(-∞, 4) ∩ [-1, 5)

Solution :

(-∞, 4) ∩ [-1, 5)

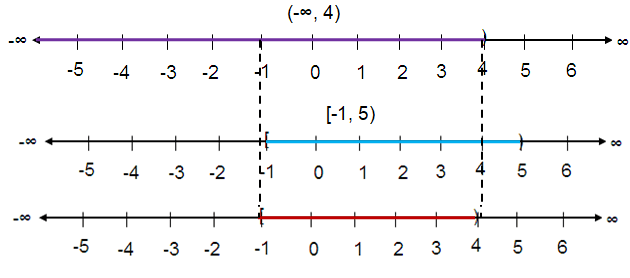
The intersection is [-1, 4).

Problem 6 :

(-∞, 4) ∪ [-1, 5)

Solution :

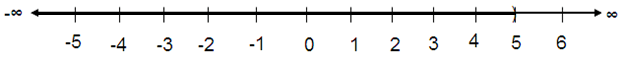
The union is (-∞, 5).

Problem 7 :

(-5/2, 3) ∩ (-1, 9/2)

Solution :

(-5/2, 3) ∩ (-1, 9/2)

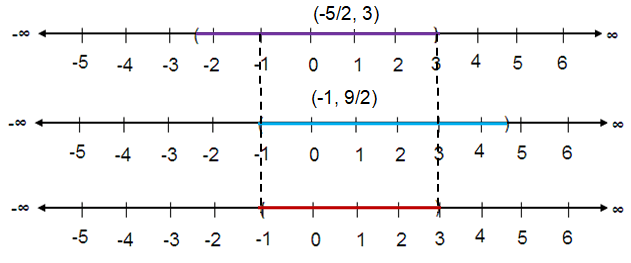
The intersection is (-1, 3).

Problem 8 :

(-5/2, 3) ∪ (-1, 9/2)

Solution :

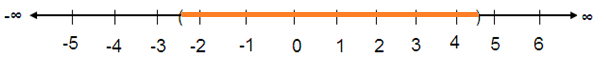
The union is (-5/2, 9/2).

Problem 9 :

(-3.4, 1.6) ∩ (-2.2, 4.1)

Solution :

(-3.4, 1.6) ∩ (-2.2, 4.1)

The intersection is (-2.2, 1.6).

Problem 10 :

(-3.4, 1.6) ∪ (-2.2, 4.1)

Solution :

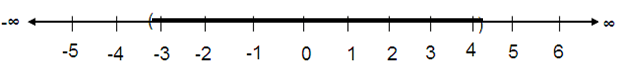
The union is (-3.4, 4.1).

Problem 11 :

(-4, 5] ∩ (0, 2]

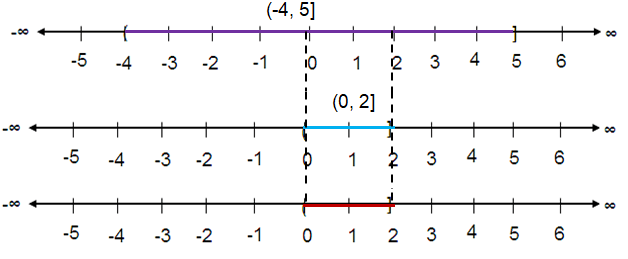
The intersection is (0, 2].

Problem 12 :

(-4, 5] ∪ (0, 2]

Solution :

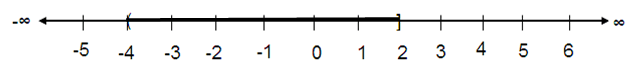
The union is (-4, 2].

Problem 13 :

(-1, 5) ∩ (0, 3)

Solution :

[-1, 5) ∩ (0, 3)

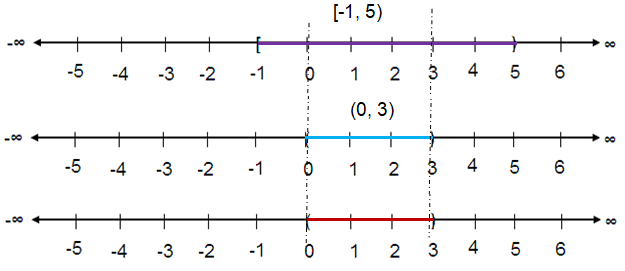
The intersection is (0, 3).

Problem 14 :

[-1, 5) ∪ (0, 3)

Solution :

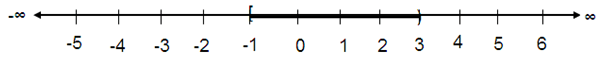
The union is [-1, 3).