TYPES OF INTERVALS IN MATHEMATICS

Open Interval (  )

Definition :

Represents the set of real numbers between a and b, but NOT including the values of a and b themselves.

Interval notation :

(a, b)

Set builder notation :

{ x| a < x < b }

Graph :

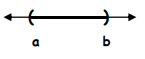
For example,

(-3, 5)

Possible values from the interval is {-2, -1, 0, 1, 2, 3, 4}

Closed Interval [  ]

Represents the set of real numbers between, and including a and b.

Definition :

Represents the set of real numbers between, and including a and b

Interval notation :

[a, b]

Set builder notation :

{ x| a ≤ x ≤ b }

Graph :

For example,

[-3, 5]

Possible values from the interval is {-3, -2, -1, 0, 1, 2, 3, 4, 5}

The end points are included.

Half Closed - Half Open Interval

Definition :

Represents the set of real numbers between a and b, including a but NOT including b. [a, b)

Represents the set of real numbers between a and b, NOT including a but including b. (a, b]

Interval notation :

[a, b)  or  (a, b]

Set builder form :

{ x| a ≤ x < b }

{ x| a < x ≤ b }

Graph :

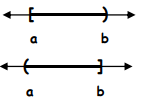
For example,

[-3, 5)

Possible values from the interval is {-3, -2, -1, 0, 1, 2, 3, 4}

(-3, 5]

Possible values from the interval is {-2, -1, 0, 1, 2, 3, 4, 5}

Infinite Interval

Write the following inequalities in interval notation and graph

Problem 1 :

x ≤ 3

Solution :

Interval notation :

(- ∞, 3]

Graph :

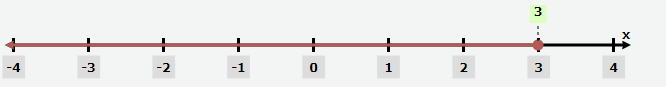
Problem 2 :

-2 < x ≤ 4

Solution :

Interval notation :

(-2, 4]

Graph :

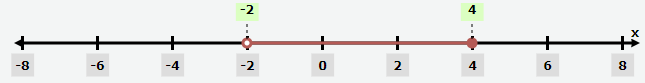
Problem 3 :

-9 ≤ x ≤ 0

Solution :

Interval notation :

[-9, 0]

Graph :

Problem 4 :

x > - 4

Solution :

Interval notation :

(4, ∞)

Graph :

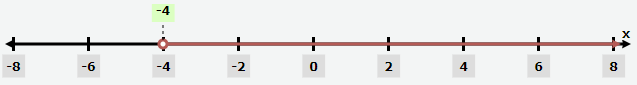
Problem 5 :

x < -3

Solution :

Interval notation :

(∞, -3)

Graph :

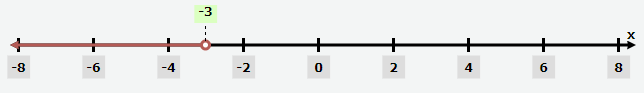
Problem 6 :

 x ≥ 6

Solution :

Interval notation :

(4, ∞)

Graph :

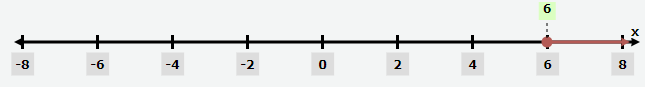
Express each of the following intervals in set-builder notation.

Problem 7 :

(2, 8)

Solution :

Both 2 and 8 are not included. So,

Set builder form :

{ x| 2 < x < 8 }

Problem 8 :

[-5, 0)

Solution :

-5 is included but 0 is not included. So,

Set builder form :

{ x| -5 ≤ x < 0 }

Problem 9 :

(3, ∞)

Solution :

3 and ∞ are not included. So,

Set builder form :

{x| 3 < x < ∞}

Problem 10 :

(- ∞, -4]

Solution :

-∞ is included but -4 not included. So,

Set builder form :

{x| -∞ < x < -4}