TRUE BEARING AND TRIGONOMETRY WORD PROBLEMS

Problem 1 :

A helicopter travels from base station S on a true bearing of 074° for 112 km to outpost A. It then travels 134 km on a true bearing of 164° to outpost B. How far is outpost from base station S ?

Solution :

Point to be remembered :

Measurements are always taken in the clockwise direction.

In triangle SAB, ∠SAB = 90°

Using Pythagorean theorem,

SB² = SA² + AB²

x² = 112² + 134²

x² = 12544 + 17956

x² = 30500

x = √30500

x = 174.64

Approximately 175 km.

Problem 2 :

Two bushwalkers set off from base camp at the same time. One walks on a true bearing of 049° at an average speed of 5 kmh^-1, while the other walks on a true bearing of 319° at an average speed of 4 kmh^-1. Find their distance apart 3 hours.

Solution :

Let t be the time taken in between AB, BC and CA

Here t = 3 hours

Distance = time x speed

AB = 3 x 5 ==> 15 km

BC = 3 x 4 ==> 12 km

AC² = AB² + BC²

x² = 15² + 12²

= 225 + 144

= 369

x = √369

x = 19.2 km

So, the distance after 3 hours is 19.2 km.

Problem 3 :

James is about to tackle an orientation course. He has been given these instruction.

• the course is triangular and starts and finishes at S.
• the first checkpoint A is in the direction 056° from S.
• the second checkpoint B is in the direction 146° from A.
• the distance from A to B is twice the distance from S to A. 
• the distance from B to S is 2.6 km.

Find the length of orientation course.

Solution :

BS² = SA² + AB²

2.6² = x² + (2x)²

6.76 = x² + 4x²

6.76 = 5x²

x² = 6.76/5

x² = 1.352

x = 1.16

2x = 2(1.16)

= 2.32

Length of the orientation course = x + 2x + 2.6

= 1.16 + 2.32 + 2.6

= 6.08 km

So, the length of the orientation is 6.08 km.

Problem 4 :

A fighter plane and helicopter set off from airbase A at the same time. The helicopter travels on a bearing of 152° and the fighter plane travels on bearing of 242° at three times the speed. They arrive bases B and C respectively, 2 hours later. IF B and C are 1200 km apart, find the average speed of the helicopter.

Solution :

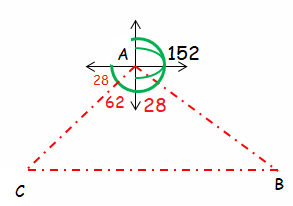
 ∠CAB = 62 + 28 ==> 90°

Distance between B and C = 1200 km

Time (t) = distance / speed

2 = 1200/speed

Speed = 1200/2

= 600 km/h

Let x be the speed to reach A to B, then 3x be the speed to reach A to C.

BC² = AC² + AB²

600² = (3x)² + x²

360000 = 9x² + x²

360000 = 10x²

360000/10 = x²

x² = 36000

x = √36000

x = 189.7 km/h

So, the required speed is approximately 190 km/h.

Problem 5 :

Two rally car drivers set off from town C at the same time. Driver A travels in the direction 63° T at 120 km/h while driver B travels in the direction 333° T at 135 km/h. How far they apart after one hour ?

Solution:

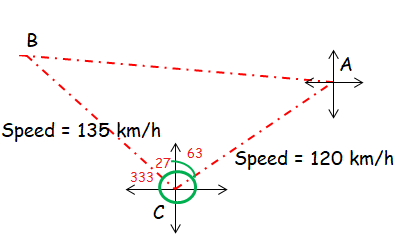
∠BCA = 27 + 63 ==> 90

Time taken to reach C to A and C to B is one hour. So, the distance covered in between CA is 120 km and CB is 135 km.

Using Pythagorean theorem,

AB² = AC² + BC²

AB² = 120² + 135²

AB² = 14400 + 18225

AB² = 32625

AB = 180.6

Approximately 181 km.

Problem 6 :

Town B is 27 km from Town A in the direction 134° T. Town C is 21 km from town B in a direction 224° T. Find the distance between A and C.

Solution :

∠ABC = 44 + 46 ==> 90

Using Pythagorean theorem,

AC² = AB² + BC²

AC² = 27² + 21²

= 729 + 441

AC² = 1170

AC = 34.2 km

So, the distance between A and C is 34.2 km.