TRIANGLE PROPORTIONALITY THEOREM

If a line is parallel to one side of a triangle and intersects the other two sides, then it divides the two sides proportionally.

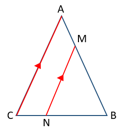
Consider the triangles NBM and CAB.

∠MNB = ∠ACB

∠NBM = ∠CBA

triangles NMB and CAB are similar, then corresponding sides will be in the same ratio.

Find the missing side indicated.

Problem 1 :

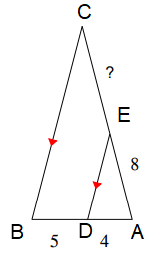
Solution :

AD/AB = AE/AC

Let EC = x, AC = 8 + x

4/(4+5) = 8/(8 + x)

4/9 = 8/(8 + x)

4(8 + x) = 8(9)

32 + 4x = 72

4x = 72 - 32

4x = 40

x = 40/4

x = 10

So, the measure of EC is 10.

Problem 2 :

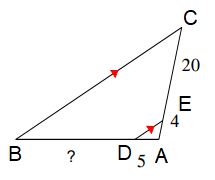
Solution :

From the figure given above

AD/AB = AE/AC

Let BD = x, AB = 5 + x

5/(5 + x) = 4/24

5/(5 + x) = 1/6

Doing cross multiplication, we get

30 = 5 + x

x = 30 - 5

x = 25

So, the measure of BD is 25.

Problem 3 :

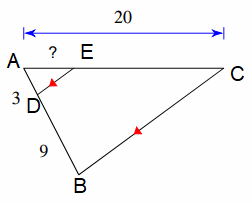
Solution :

From the figure given above

AD/AB = AE/AC

Let AE = x

3/(3 + 9) = x/20

3/12 = x/20

3(20) = 12x 

60 = 12x

x = 60/12

x = 5

So, the measure of AE is 5.

Problem 4 :

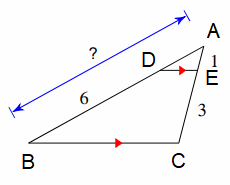
Solution :

From the figure given above

AD/AB = AE/AC

Let AD = x

x/(6 + x) = 1/(1 + 3)

x/(6 + x) = 1/4

4x = 6 + x

4x - x = 6

3x = 6

x = 6/3

x = 2

AB = 6 + x

AB = 6 + 2 ==> 8

So, the measure of AB is 8.

Problem 5 :

In the diagram,  PQ||NR . MQ = 42, MN = 13, and NP = 8.  Find RQ & MR.  

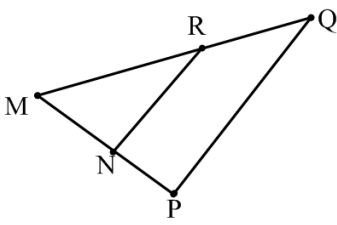
Solution :

MN / MP = MR / MQ

MP = MN + NP

MP = 13 + 8

MP = 21

Let x = MR

13/21 = x/42

x = 13(41)/21

x = 26 = MR

MQ = MR + RQ

42 = 26 + RQ

42 - 26 = RQ

RQ = 16

Problem 6 :

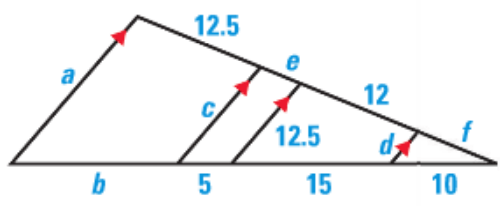
Solution :

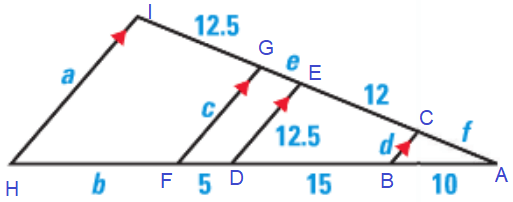
Considering triangles ABC, ADE

Considering triangles ABC, AGF

Considering triangles AGF and AIH

GF/IH = FA/HA = AG/AI

c/a = 30/(b+30) = (12+e+f)/(12.5+12+e+f)

15/a = 30/(b+30) = (12+4+8)/(24.5+ 4+8)

15/a = 30/(b+30) = 24/36.5

15/a = 24/36.5 and 30/(b+30) = 24/36.5

a = 22.81 and b + 30 = 45.62 ==> b = 15.62