TRIANGLE MIDSEGMENT THEOREM

The segment joining the midpoints of two sides of a triangle is parallel to and half the length of the third side.

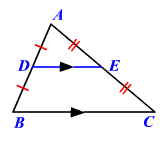
In triangle ABC, D and E are the midpoints of the sides AB and AC respectively. Then,

AD = DB and AE = DC and DE || BC

Considering triangles ADE and ABC,

∠ADE = ∠ABC

∠AED = ∠ACB

So, we say triangle ADE ∼ triangle ABC

Problem 1 :

Solve for x.

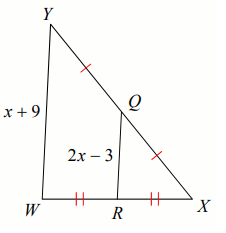
Solution:

Using Midsegment Theorem,

2(QR) = YW

2(2x - 3) = x + 9

4x - 6 = x + 9

4x - x = 9 + 6

3x = 15

x = 5

Problem 2 :

Solve for x.

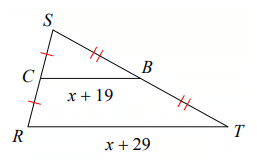
Solution:

Using Midsegment Theorem,

2(CB) = RT

2(x + 19) = x + 29

2x + 38 = x + 29

2x - x = 29 - 38

x = -9

Problem 3 :

Solve for x.

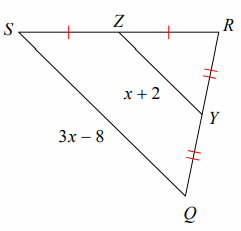
Solution: 

Using Midsegment Theorem,

2(ZY) = SQ

2(x + 2) = 3x - 8

2x + 4 = 3x - 8

3x - 2x = 8 + 4

x = 12

Problem 4 :

Solve for x.

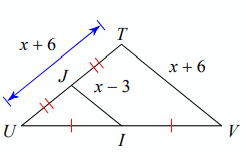
Solution: 

Using Midsegment Theorem,

2(JI) = TV

2(x - 3) = x + 6

2x - 6 = x + 6

2x - x = 6 + 6

x = 12

Problem 5 :

Find LN:

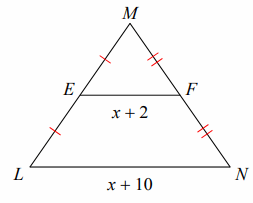
Solution: 

Using Midsegment Theorem,

2(EF) = LN

2(x + 2) = x + 10

2x + 4 = x + 10

2x - x = 10 - 4

x = 6

Finding LN:

LN = x + 10

LN = 6 + 10

LN = 16

Problem 6 :

Find RQ:

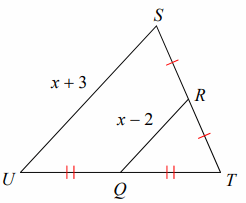
Solution: 

Using Midsegment Theorem,

2(RQ) = SU

2(x - 2) = x + 3

2x - 4 = x + 3

2x - x = 3 + 4

x = 7

Find RQ:

RQ = x - 2    

RQ = 7 - 2

RQ = 5

Problem 7 :

Find SR:

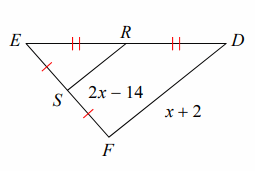
Solution: 

Using Midsegment Theorem,

2(SR) = FD

2(2x - 14) = x + 2

4x - 28 = x + 2

4x - x = 2 + 28

3x = 30

x = 10

Find SR:

SR = 2x - 14

SR = 2(10) - 14

SR = 6

Problem 8 :

Find VW :

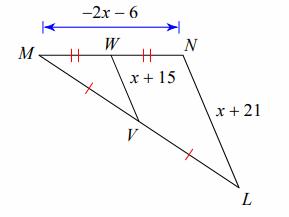
Solution: 

Using Midsegment Theorem,

2(VW) = LN

2(x + 15) = x + 21

2x + 30 = x + 21

2x - x = 21 - 30

x = -9

Find VW:

VW = x + 15

VW = -9 + 15

VW = 6