TRANSLATING POINTS ON A COORDINATE PLANE

Problem 1 :

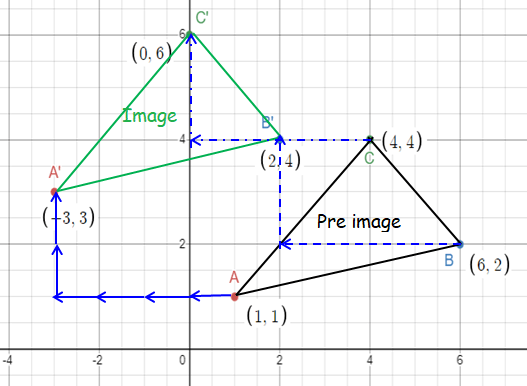
a. On the graph, draw and label ΔABC, whose vertices have the coordinates A(1 , 1), B(6 , 2), and C(4 , 4).

b. Under the translation (x , y) -->(x - 4, y + 2), on the same graph, draw and label ΔA`B`C`.

c. Map the Translation

A(1 , 1) -->

B(6 , 2) -->

C(4 , 4) -->

Solution :

a) & b)

c)

A (1 , 1) --> A' (1 - 4, 1 + 2) ==> A'(-3, 3)

B (6 , 2) --> B' (6 - 4, 2 + 2) ==> B'(2, 4)

C (4 , 4) --> C' (4 - 4, 4 + 2) ==> C'(0, 6)

Problem 2 :

Graph the original triangle and the image of ΔDEF under the translation T_{3 , -1}.

b. Rewritten as:

c. Map the translation:

D(0 , 2)

E(1 , -3) 

F(3 , -1)

Solution :

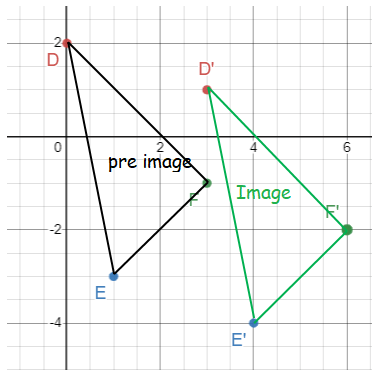
c) D(0 , 2) --> D' (0+3, 2-1) ==> D'(3, 1)

E(1 , -3) --> E' (1+3, -3-1) ==> E'(4, -4)

F(3 , -1) --> F' (3+3, -1-1) ==> F'(6, -2)

Problem 3 :

Rewrite the translation in a different form:

a. T_{-2, 5}  __________

b. (x, y) --> (x + 4, y – 1) - ___________

Solution :

a. T_{-2, 5}  --> (x - 2, y + 5)

b. (x, y) --> (x + 4, y – 1) --> T_{4, -1}

Problem 4 :

Does the image remain congruent after a translation? Explain your answer.

Solution :

Translation of point means, shifting the point from one place to other. So, the size of the image will not be changed. Then the image will remain congruent.

Problem 5 :

 The rule for the translation so the image of A is A` is:

A(2 , 5) --> A`(-1 , 1)

a) T_{1, -4}         b) T_{-3 , -4}       c) T_{3, 4}       d) T_-1,4

Solution :

Option a :

A(2 , 5) --> A`(2 + 1, 5 - 4) ==> A'(3, 1)

Option b :

A(2 , 5) --> A`(2 - 3, 5 - 4) ==> A'(-1, 1)

So, option b is correct.

Problem 6 :

Which point is the image of P(4 , -3) under the translation

P(x , y) --> `(x - 4, y) ?

a) P`(-8 , 0)     b) P` (8 , -3)     c) P`(0 , -3)    d) P`(0 , 0)

Solution :

Original point is P(4, -3). This point is to be translated to 4 units left and no vertical translation.

P(4, -3) ==> P' (4 - 4, -3 - 0) ==> P'(0, -3)

Problem 7 :

 Find the image of with the given translation rule.

T_{2 , -3}

H (-2, 0) --> 

O(0 , 0) --> 

T (0 , 4) --> 

Solution :

H (-2, 0) --> H' (-2 + 2, 0 - 3) ==> H'(0, -3)

O(0 , 0) --> O' (0 + 2, 0 - 3) ==> O'(2, -3)

T (0 , 4)  --> T' (0 + 2, 4 - 3) ==> T'(2, 1) 

Problem 8 :

The coordinates of ΔABC are

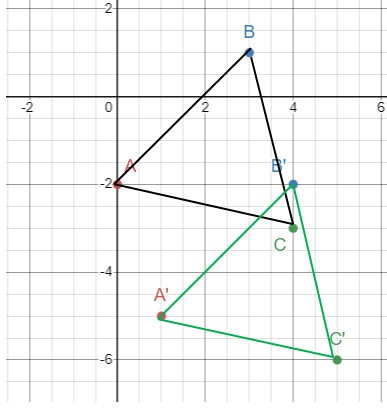
A(0 , -2), B(3 , 1), and C(4 , -3).

Graph and label these points.

b. Under the translation (x , y) --> (x +1, y - 3), draw and label ΔA`B`C`.

c. Map the Translation

Solution :

A(0 , -2) --> A'(0 + 1, -2 - 3) ==> A'(1, -5)

B(3 , 1) --> B'(3 + 1, 1 - 3) ==> B'(4, -2)

C(4 , -3) --> C'(4 + 1, -3 - 3) ==> C'(5, -6)

Problem 9 :

Map the translation of ΔBUG under the rule given below.

T_{-2 , 4}

B(-2 , -3) --->

U(1 , 0) ---->

G(3 , -4) --->

Solution :

B(-2 , -3) ---> B' (-2 - 2, -3 + 4) ==> B' (-4, 1)

U(1 , 0) ---> U' (1 - 2, 0 + 4) ==> U' (-1, 4)

G(3 , -4)  ---> G' (3 - 2, -4 + 4) ==> G' (1, 0)

Problem 10 :

Which of the following is the rule of the translation in which every point moves 6 units to the right on a graph?

a) (x , y) --> (x , y + 6)          b) (x , y) -->(x +6, y)

c) (x , y) --> (x +6, y + 6)      d) (x , y) -->(x -6, y)

Solution :

Observing option b, the value of x moved right 6 units and there is no change vertically. So, the answer is 

(x , y) -->(x +6, y)

Problem 11 :

Which quadrant does the point (-2, 4) lie in?

Solution :

(-2, 4) looks like (-x, y)

So, it lies in the second quadrant.