TRANSFORMATIONS WITH QUADRATIC FUNCTIONS

Problem 1 :

The graph f(x) = x² has a vertical compression of by a factor of 1/2, is shifted up 6, and right 5. What is the equation of the function after the transformation?

Solution:

Vertical compression by the factor of 1/2, shifting up 6 and right 5.

Here a = 1/2, k = 6 and h = 5

y = a(x - h)² + k

f(x) = 1/2(x - 5)² + 6

Problem 2 :

Describe in words how the graph of g(x) = -5(x + 2)² - 3 would be transformed from the parent function f(x) = x².

Solution:

y = a(x - h)² + k

g(x) = -5(x + 2)² - 3

g(x) = -5(x - (-2))² - 3

Here h = - 2, k = -3, a = 5 and reflection about x-axis.

Accordingly order of transformation :

• Vertical stretch with the factor of 5.
• Reflection about x-axis.
• Moving left 2 units and moving down 3 units.

Problem 3 :

Translate y = x² + 2x + 1 four units to the right and 1 unit down. What is the equation of the new function, in vertex form?

Solution:

y = x² + 2x + 1

In order to do the transformation, we can convert the standard form to vertex form.

y = x² + 2 ⋅ x ⋅1 + 1² - 1² + 1

y = (x + 1)² - 1 + 1

y = (x + 1)²

Moving 4 units right and 1 unit down.

y = (x + 1)²

y = (x + 1 - 4)² - 1

y = (x - 3)² - 1

Problem 4 :

Which function includes a translation of 3 units to the left?

a. f(x) = (x + 3)² + 1           b. f(x) = 3x² + 1

c. f(x) = (x - 3)² + 1           d. f(x) = (x + 1)² - 3

Solution:

When we translate a function to the left by a certain number of units, we subtract that number from the x-values.

In this case, subtracting 3 units from x would result in a translation to the left.

f(x) = (x - (-3))² + 1   

Here h = -3, moving the graph horizontally 3 units to the left. So, option a is correct.

Problem 5 :

Which equation shows a translation of 3 left and vertical compression by a factor of 2 to the graph of y = x²?

a. y = 2(x - 3)²      b. y = 2(x + 3)²

c. y = 1/2(x - 3)²         d. y = 1/2(x + 3)²

Solution:

Move the vertex to (h, k) equals (-3, 0) and stretch from that point in the vertical direction by 2. So, a = 2

y = a(x - h)² + k

f(x) = 2(x + 3)²

So, option (b) is correct.

Problem 6 :

List the sequence of steps required to graph the function

f(x) = -(x + 4)² - 6

a. horizontal translation 4 units to the right, vertical compression by a factor of 1, vertical translation 6 units down.

b. horizontal translation 4 units to the right, reflection in x-axis, vertical translation 6 units down.

c. horizontal translation 4 units to the left, vertical translation 6 units up, reflection in x-axis.

d. horizontal translation 4 units to the left, reflection in x-axis, vertical translation 6 units down.

Solution:

f(x) = -(x + 4)² - 6

Since we have negative coefficient, there should be reflection across x-axis.

f(x) = -(x - (-4))² - 6

Here h = -4 and k = -6

So, we have to move the graph 4 units left and 6 units down.

So, option (d) is correct.

Problem 7 :

Consider a parabola P that is congruent to y = x², opens upward, and has vertex (-1, 3). Now find the equation of a new parabola that results if P is reflected in the x-axis and translated 3 units down.

a. y = -(x + 4)² + 3         b. y = (x - 1)² + 6

c. y = -(x + 1)²             d. y = -(x - 2)² + 3

Solution:

y = a(x - h)² + k

Vertex is at (-1, 3)

y = (x - (-1))² + 3

y = (x + 1)² + 3

Using the given transformation :

Reflection across x-axis, translating the graph 3 units down.

y = -(x + 1)² + 3 - 3

y = -(x + 1)²

So, option (c) is correct.

Problem 8 :

The graphs of y = x² and another parabola are shown below. What is a possible equation for the second parabola?

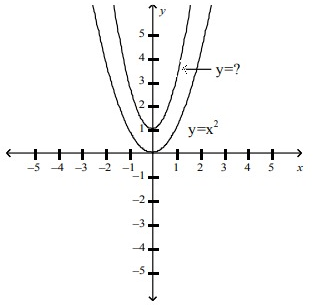
a. y = 2x² + 1        b. y = 1/2x² + 1       c. y = 2(x + 1)²

d. y = -2x² - 1

Solution:

By comparing the new graph with the graph of parent function, it is moved 1 unit up and there is vertical stretch because the wide is decreased.

Option c, y = 2(x + 1)² will be correct.