TRANSFORMATIONS OF SQUARE ROOT FUNCTIONS

Graph each transformation of the parent function

f(x) = √x

Analyze the effect of the transformation on the graph of the parent function

Problem 1 :

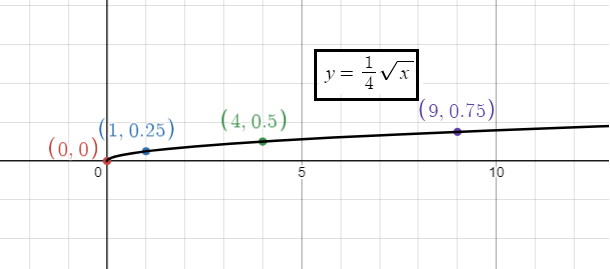
y = (1/4)√x 

Solution :

Comparing the function with y = a√b(x - h) + k

a = 1/4, b = 1, h = 0 and k = 0

Describing the transformation :

• 0 < a < 1, there is vertical shrink of 1/4 units.

Problem 2 :

y = -2√x 

Solution :

Comparing the function with y = a√b(x - h) + k

a = 2, b = 1, h = 0 and k = 0

Describing the transformation :

• a > 1, there is vertical stretch of 2 units.

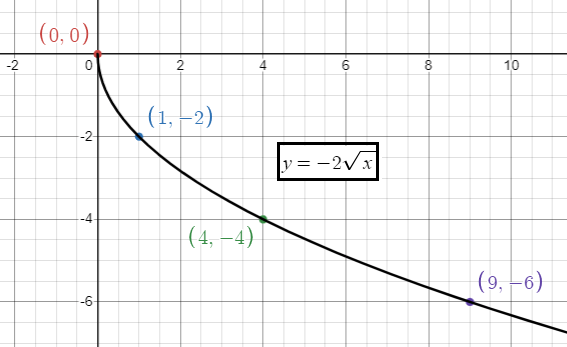
Problem 3 :

y = 3√(x + 2)

Solution :

Comparing the function with y = a√b(x - h) + k

y = 3√(x - (-2))

a = 3, b = 1, h = -2 and k = 0

Describing the transformation :

• a > 3, there is vertical stretch of 3 units.
• h = -2, move the graph horizontally 2 units left.

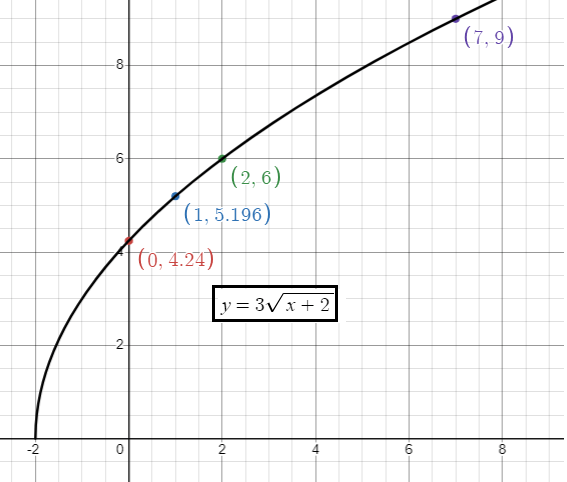
Problem 4 :

y = √-5x

Solution :

Comparing the function with y = a√b(x - h) + k

y = √-5x

a = 1, b = 5, h = 0 and k = 0

Describing the transformation :

• b = 5 > 1, there is horizontal compression.
• Sign of b is negative, so there is a reflection across y-axis.

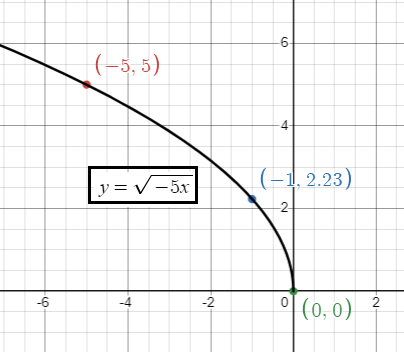
Problem 5 :

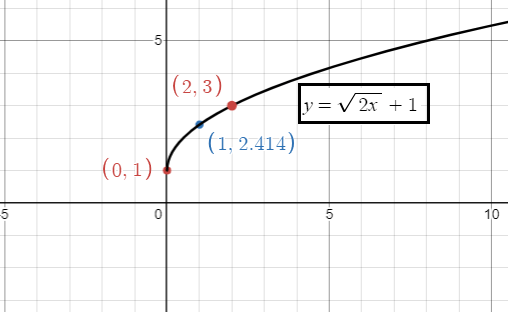
y = √2x + 1

Solution :

Comparing the function with y = a√b(x - h) + k

y = √2x + 1

a = 1, b = 2, h = 0 and k = 1

Describing the transformation :

• b = 2 > 1, there is horizontal compression.
• k = 1, move the graph up 1 unit.

Problem 6 :

A company makes steel food cans of different sizes. All of the cans are 10 cm tall, but their radii vary. The equation r = 0.18√V gives the radius of a can based on the can’s volume.

a. Describe this equation as a transformation of y = √x.

b. The volume of one size of can is 300 cubic centimeters. What is the radius of this can? Round to the nearest hundredth.

Solution :

a)

r = 0.18√V

Here a = 0.18, 0 < a < 1

• There is vertical compression of 0.18 units.
  
  

b) When V = 300

r = 0.18√V

Applying the value of V, we get

r = 0.18√300

r = 0.18 (17.32)

r = 3.117

Problem 7 :

The quality control supervisor at a car part factory uses the equation

y = √ (1/10) x + 20

to determine the number of parts, y, to inspect based on the number manufactured, x.

a. Describe this equation as a transformation of y = √x.

b. The supervisor determined that 55 parts should be inspected. How many were manufactured?

Solution :

y = √(1/10) x + 20

a) Here b = 1/10

0 < b < 1, there is horizontal stretch of 0.1 units

b) When y = 55

55 = √(1/10) x + 20

55 - 20 = √(1/10) x

(35)² = (1/10) x

1225 = (1/10) x 

x = 1225(10)

x = 12250