TRANSFORMATIONS OF LINEAR AND ABSOLUTE VALUE FUNCTIONS

write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

Problem 1 :

f(x) = x − 5; translation 4 units to the left

Solution :

f(x) = x − 5

Given transformation :

Translation 4 units to the left

Let g(x) be the new function after the transformation.

f(x - (-4)) = x - (-4) − 5

= x + 4 - 5

g(x) = x - 1

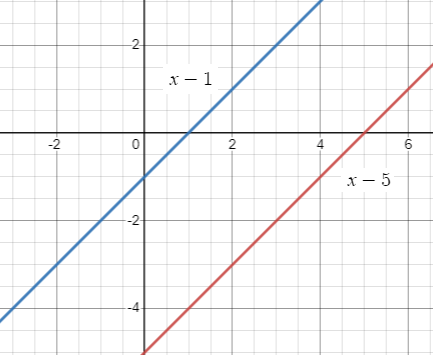
Problem 2 :

f(x) = x + 2; translation 2 units to the right

Solution :

f(x) = x + 2

Given transformation :

Translation 2 units to the right

Let g(x) be the new function after the transformation.

f(x - 2) = x - 2 + 2

g(x) = x

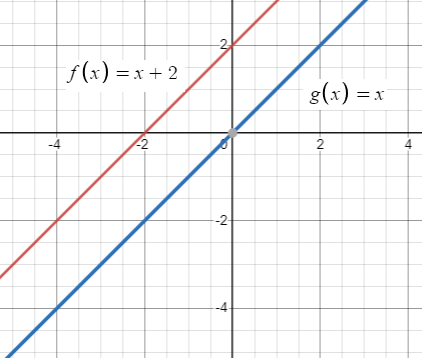
Problem 3 :

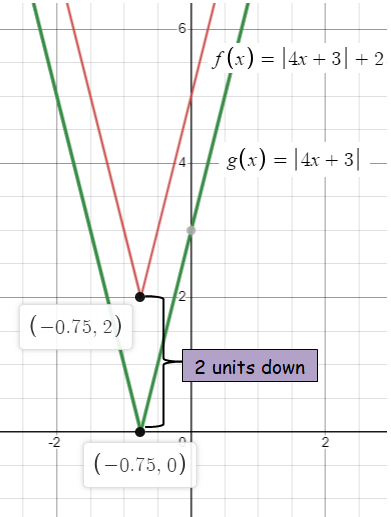
f(x) = ∣4x + 3 ∣ + 2; translation 2 units down

Solution :

f(x) = ∣4x + 3 ∣ + 2

Given transformation :

translation 2 units down

Let g(x) be the new function after the transformation.

f(x) - 2 = ∣4x + 3 ∣ + 2 - 2

g(x) = |4x + 3|

Problem 4 :

f(x) = 2x − 9; translation 6 units up

Solution :

f(x) = 2x - 9

Given transformation :

translation 6 units up

Let g(x) be the new function after the transformation.

f(x) + 6 = 2x - 9 + 6

g(x) = 2x - 3

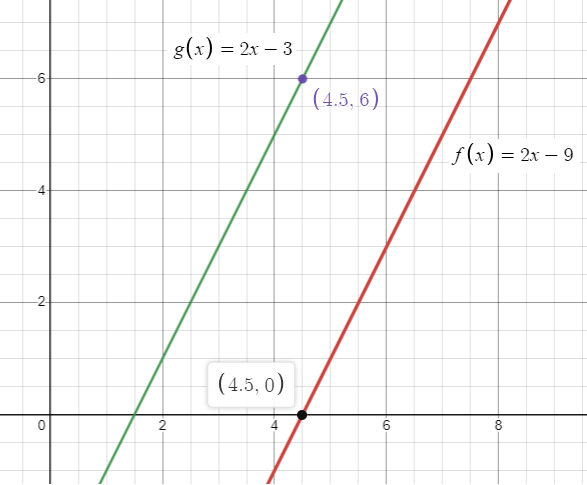
Problem 6 :

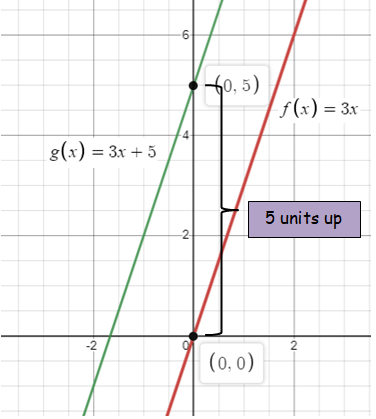
f(x) = 3x; translation 5 units up

Solution :

Given transformation :

translation 5 units up

Let g(x) be the new function after the transformation.

f(x) + 5 = 3x + 5

g(x) = 3x + 5

Problem 7 :

f(x) = ∣x∣ − 3; translation 4 units to the right

Solution :

Given transformation :

translation 4 units to the right.

Let g(x) be the new function after the transformation.

f(x - 4) = ∣x - 4∣ − 3

= ∣x - 4∣ − 3

g(x) = ∣x - 4∣ − 3

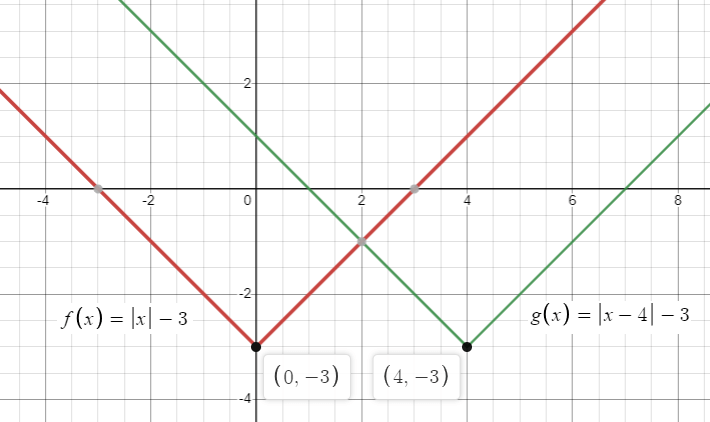
Problem 8 :

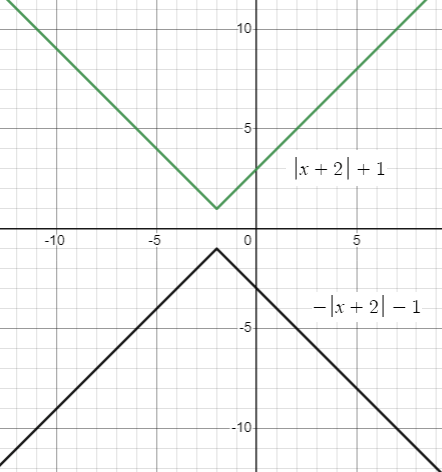
f(x) = −∣x + 2 ∣ − 1; reflection in the x-axis

Solution :

Given transformation :

reflection in the x-axis

Let g(x) be the new function after the transformation.

f(x) = −∣x + 2 ∣ − 1

-f(x) = -[−∣x + 2 ∣ − 1]

= ∣x + 2 ∣ + 1

g(x) = ∣x + 2 ∣ + 1

Problem 9 :

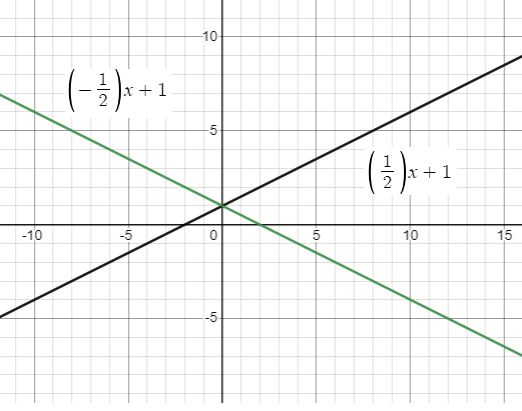
f(x) = (1/2) x + 1; reflection in the y-axis

Solution :

Given transformation :

reflection in the y-axis

Let g(x) be the new function after the transformation.

f(-x) = (1/2) (-x) + 1

g(x) = -(1/2) (x) + 1

write a function g whose graph represents the indicated transformations of the graph of f. 

Problem 10 :

f(x) = x; vertical stretch by a factor of 2 followed by a translation 1 unit up

Solution :

f(x) = x

Vertical factor 2 units and vertical translation of 1 unit up.  Let the new function will be g(x).

f(x) = 2x + 1

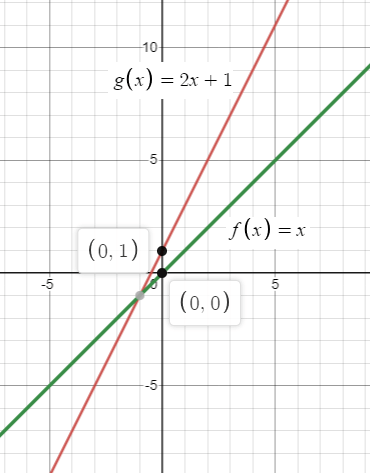
Problem 11 :

f(x) = x; translation 3 units down followed by a vertical shrink by a factor of 1/3

Solution :

f(x) = x

Translation of 3 units down and vertical shrink of 1/3. Let the new function will be g(x).

g(x) = (1/3) x + 3

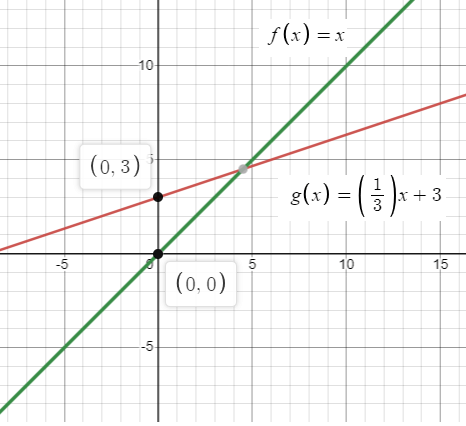
Problem 12 :

f(x) = ∣x∣; translation 2 units to the right followed by a horizontal stretch by a factor of 2

Solution :

f(x) = ∣x∣

Translation of 2 units right and horizontal stretch by the factor of 2. Let g(x) be the new function.

First we have to do stretch and then do the translation.

f((1/2) x - 2) = ∣(1/2)x - 2|

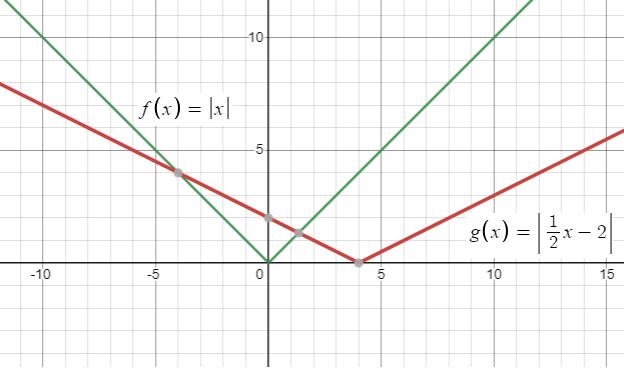
Problem 13 :

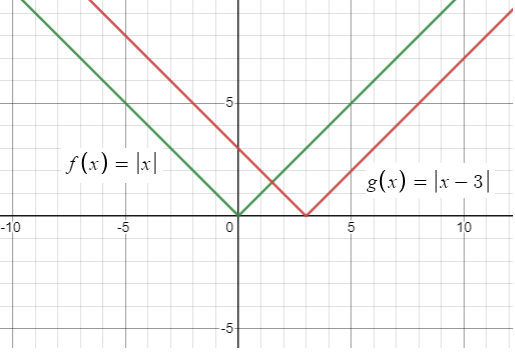
f(x) = ∣x∣ ; reflection in the y-axis followed by a translation 3 units to the right

Solution :

f(x) = ∣x∣

Reflection in the y-axis and then translation. Replace x as -x.

Let the new function will be g(x). After applying the reflection, we get

g(x) = |-x| ==> |x|

After the translation,

g(x) = |x - 3|