TRANSFORMATION OF QUADRATIC FUNCTIONS WORKSHEET

Problem 1 :

What are the transformations on the function

y = 2x² + 4x - 15

Problem 2 :

The function from y = 2x² + 20x - 22, is shifted 3 units up and 2 to the left. What is the new equation for y?

Problem 3 : 

Translate the graph of f(x) = x² four (4) units to the left, three (3) units up and stretch the graph by a factor of 2. Which of the following is the function after the transformations?

A. f(x) = 1/2(x + 4)² + 3             B. f(x) = 1/2(x - 3)² - 4

C. f(x) = 2(x + 4)² + 3                D. f(x) = 2(x - 3)² - 4

Problem 4 :

Translate y = x² + 2x + 1 four units to the right and 1 unit down. What is the equation of the new function, in vertex form?

Problem 5 :

The graph f(x) = x² has a vertical compression of by a factor of 1/5 and is shifted down 8. What is the equation of the function after the transformation?

Problem 6 :

Describe in words how the graph of g(x) = -3(x + 5)² would be transformed from the parent function f(x) = x².

Problem 7 :

Given the graph of h(x), fill in the requested information:

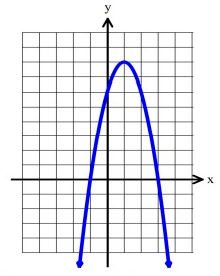
Transformations:

Vertex:

y-intercept:

Roots:

Domain:

Range:

Max/Min:

Problem 8 :

Compare the functions, f(x) and g(x), and explain how the graph of f(x) = x² - 4x + 4 is related to the graph of g(x) = x² - 4x - 2.

A. f(x) is vertically stretched to make g(x)

B. f(x) is translated 6 units left to make g(x)

C. f(x) is translated down 6 units to make g(x)

D. f(x) is compressed vertically to make g(x)

Solution :

1. Answer :

y = 2x² + 4x - 15

= 2(x² + 2x) - 15

= 2[(x + 1)² - 1] - 15

= 2(x + 1)² - 2 - 15

= 2(x + 1)² - 17

h = -1 and k = -17

Parent function y = x²

Describing transformation :

Vertically stretch a factor of 2, moving the curve left 1 units and down 17 units.

2. Answer :

y = 2x² + 20x - 22

y = x² + (20/2)x - (22/2)

= x² + 10x - 11

= x² + 2(x)(5) - 11

= x² + 2(x)(5) + 5² - 11 - 5²

y = (x + 5)² - 36

3 units up and 2 units left.

y = (x + 5 - 2)² - 36 + 3

y = (x + 3)² - 33

3. Answer :

Move the vertex to (h, k) equals (-4, 3) and stretch from that point in the vertical direction by 2. So, a = 2

y = a(x - h)² + k

Stretch factor of 2, 4 units left and 3 units up.

a = 2, h = -4 and k = 3

= 2(x - (-4))² + 3

y = 2(x + 4)² + 3

So, option (C) is correct.

4. Answer :

y = x² + 2x + 1

4 units right and 1 unit down. So, +4 and -1

Converting the given equation in the form

y = a(x - h)² + k

= x² + 2 x (1) + 1² - 1² + 1

= (x + 1)² - 1 + 1

y = (x + 1)²

Applying the required changes :

y = (x + 1 - 4)² - 1

y = (x - 3)² - 1

So, vertex form is y = (x - 3)² - 1.

5. Answer :

Move the vertex to (h, k) equals (0, -8) and stretch from that point in the vertical direction by 1/5. So, a = 1/5

y = a(x - h)² + k

y = 1/5(x - 0)² - 8

f(x) = 1/5x² - 8

6. Answer :

y = a(x - h)² + k

g(x) = -3(x + 5)² 

= -3(x - (-5))² 

Describing the transformation :

• Vertically stretched with the factor of 3
• Reflection across x-axis
• Shifting the graph 5 units left.

7. Answer :

Transformations:

Since the parabola opens down, reflection across x-axis happened. Moving the graph 1 unit right and 8 units up.

Vertex:

Vertex (h, k) = (1, 8)

y-intercept:

y-intercept = (0, 6)

Roots:

Roots = (-1, 0) and (3, 0)

Domain:

All real number.

x € R

Range:

{y| y ≤ 8}

Max/Min:

Max = 8

8. Answer :

f(x) = x² - 4x + 4

g(x) = x² - 4x - 2

Converting into vertex form

-6, so the graph has been shifted 6 units down.