SYSTEMS OF EQUATIONS AND INEQUALITIES PRACTICE

Problem 1 :

Only chocolate and vanilla ice cream cones are sold at an ice cream store. In one day, the number of chocolate cones are sold was 1 more than 4 times the number of Vanilla cones sold. A total of 121 cones were sold that day. 

• Write equations to determine the number of chocolate cones sold that day.
• Use equations to determine the number of chocolate cones sold that day.

Solution :

Let v be the number of Vanilla cones sold and c be the number of chocolate cones sold.

c = 4v + 1

Total number of cones sold = 121

c + v = 121

Applying the value of c in c + v = 121, we get

4v + 1 + v = 121

5v + 1 = 121

5v = 120

v = 120/5

v = 24

Applying the value of v, we get

c = 121 - 24

c = 97

So, 97 chocolate cones are sold.

Problem 2 :

The math club sells candy bars and drinks during foot ball games.

• 60 candy bars and 110 drinks will sell for $265
• 120 candy bars and 90 drinks will sell for $270

How much does each candy bar sell for ?

Solution :

Let c be the cost of each candy bars and d be the cost of each drinks.

60c + 110d = 265 -----(1)

120c + 90d = 270  -----(2)

(1) x 2 - (2) ==>

(120c + 220d) - (120c + 90d) = 530 - 270

220d - 90d = 260

130d = 260

d = 2

Applying the value of d in (1), we get

60c + 110(2) = 265

60c = 265 - 220

60c = 45

c = 45/60

c = 0.75

So, each candy bar should sold out for 0.75.

Problem 3 :

Two times Antonio's age plus three times Sarah's age equals 34. Sarah's age is also five times Antonio's age. How old is Sarah ?

Solution :

Let S be Sarah's age and A be Antonio's age.

2A + 3S = 34 -----(1)

S = 5A -----(2)

Applying the value of S in (1), we get

2A + 3(5A) = 34

2A + 15A = 34

17A = 34

A = 2

Applying the value of A, we get

S = 5(2)

S = 10

So, Sarah's age is 10.

Problem 4 :

Paul sells chocolate chip cookies and peanut butter cookies. 

• Baking a batch of chocolate chip cookies takes 1.75 cups of flour and 2 eggs.
• Baking a batch of peanut chip cookies takes 1.25 cups of flour and 1 egg.
• Paul has 10 cups of flour and 12 eggs.
• He makes $4 profit per batch and chocolate chip cookies.
• He makes $2 profit per batch and peanut butter cookies.

How many batches of peanut butter cookies should Paul make to maximize his profit ?

a)  1     b)  2     c)   5    d)  8

Solution :

Let x be number of batches of chocolate chip cookies.

Let y be number of batches of peanut chip cookies.

1.75x + 1.25y ≤ 10

2x + 1y ≤ 12

Profit function = 4x + 2y

So, number of batches of peanut butter chips is 5.

Problem 5 :

Which ordered pair is in the solution set of the system of inequalities shown in the graph given below.

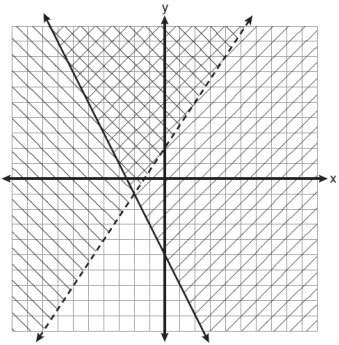
a)  (-2, -1)     b)  (-2, -4)     c)   (-2, 2)    d)  (2, -2)

Solution :

By observing the overlapping region, it is in the 2nd quadrant. Points in the second quadrant will be in the form of (-x, y). In that case, option c is correct.

Problem 6 :

Which is the graph of the solution of the system of inequalities ?

x - 2y ≤ 10

2x + y > 0

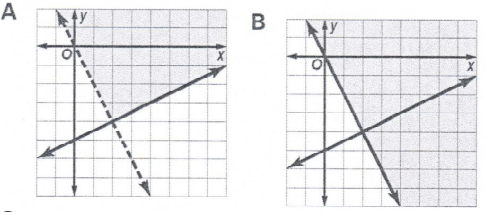
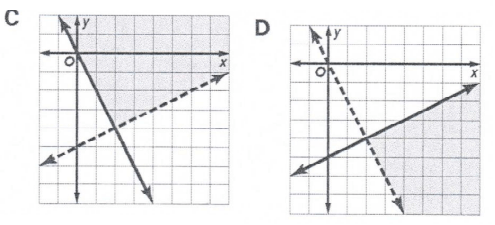
Solution :

If the shaded region is the solution, then all he points from the shaded region should satisfy the given system of equations.

Option a :

(2, -1)

So, option a is the correct answer.

Problem 7 :

Lucy and Barbara began saving money the same week.  The table below shows the models for the amount of money Lucy and Barbara had saved after x weeks.

After how many weeks will Lucy and Barbara have the same amount of money saved ?

a)  1.1 weeks      b)  1.7 weeks     c)   8 weeks    d)  12 weeks

Solution :

When f(x) = g(x), then they will save the same amount.

10x + 5 = 7.5x + 25

10x - 7.5x = 25 - 5

2.5x = 20

x = 20/2.5

x = 8

So, in 8 weeks they will save the same amount of money.

Problem 8 :

Which ordered pair is not in the solution set of 

y > 2x + 1

a)  (1, 4)     b)  (1, 6)    c)   (3, 8)    d)  (2, 5)

Solution :

y > 2x + 1

So, (2, 5) is not a solution of the given inequality.

Problem 9 :

What scenario could be modeled by the graph below ?

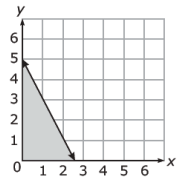
a)  The number of pounds of apples, y,  minus two times the number of pounds of oranges x, is at most 5.

b)  The number of pounds of apples, y minus half the number of pounds of oranges x, is at most 5.

c)  The number of pounds of apples, y plus two times the number of pounds of oranges x, is at most 5.

d)  The number of pounds of apples, y plus half the number of pounds of oranges x, is at most 5.

Solution :

Selecting two points from the line, (0, 5) and (1, 3).

Slope = (3 - 5)/(1 - 0)

= -2/1

m = -2

y = -2x + 5

So, option a is correct.

Problem 10 :

James is at a gift sale where everything costs $4 (included tax)

• James has $50
• James has atleast 28 remaining when he is finished buying gifts 

What is the greatest number of gifts he can buy ?

Solution :

Cost of each product = $4

Let x be the number of products he buys.

4x < (50 - 28)

4x < 22

x < 22/4

x < 5.5

So, he can buy 5 products maximum.