SURFACE AREA AND VOLUME WORD PROBLEMS

Problem 1 :

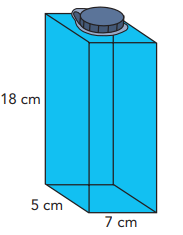
Savannah has a water bottle that is a rectangular prism. The bottle measures 7 centimeters by 5 centimeters by 18 centimeters and she filled it completely with water. Then, she drank 1/4 of the volume of water in her water bottle.

How many cubic centimeters of water were left in the water bottle?

Solution :

Capacity of bottle = Volume of rectangular prism

= length x width x height

= 18 x 5 x 7

= 630 cm³

After she drank 1/4 of the capacity, she will left over with 3/4 of the bottle

Quantity of water remaining = 3/4 of 630

= 472.5 cm³

Problem 2 :

A rectangular prism has a square base with edges measuring 8 inches each. Its volume is 768 cubic inches.

a) Find the height of the prism.

b) Find the surface area of the prism.

Solution :

a)  Volume of prism = Base area x height

768 = 8² x height

height = 768/64

= 12 cm

b)  Surface area of prism = perimeter x height

Perimeter of square base = 4(8)

= 32

Surface area of prism = 32 x 12

= 3072 cm²

Problem 3 :

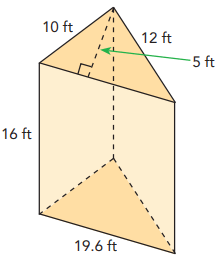
A triangular prism has the measurements shown.

a) Find the volume of the prism.

b) Find the surface area of the prism

Solution :

a)

Volume of the triangular prism = base area x height

Base area = 1/2 x base x height

= 1/2 x 19.6 x 5

= 49 ft²

Volume = 49 x 16

= 784 ft³

b)  Surface area of the triangular prism = Perimeter  x height

= (10 + 12 + 19.6) x 16

= 665.6 ft²

Problem 4 :

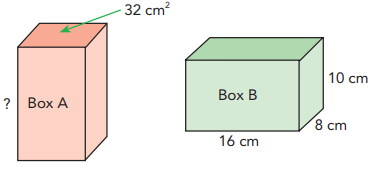
The volume of Box A is 2/5 the volume of Box B. What is the height of Box A if it has a base area of 32 square centimeters?

Solution :

Volume of box B = length x width x height

= 16 x 8 x 10

= 1280

Volume of box A = 2/5 of volume of box B

Volume of box A = ((2/5) x base area x height

1280 = (2/5) x 32 x height

height = 100 cm

Problem 5 :

The ratio of the length to the width to the height of an open rectangular tank is 10 : 5 : 8. The height of the tank is 18 feet longer than the width.

a) Find the volume of the tank.

b) Find the surface area of the open tank.

Solution :

a)  Let 10x, 5x and 8x be length, width and height of the rectangular tank respectively.

height = width + 18

8x = 5x + 18

8x - 5x = 18

3x = 18

x = 6

length (10x) = 60 ft, width (5x) = 30 ft and height (8x) = 48 ft

a)  Volume = 60 x 30 x 48

= 86400 ft³

b) Surface area of the tank = perimeter of base x height

= 2(60 x 30 + 30 x 48 + 48 x 60)

= 12240 ft²

Problem 6 :

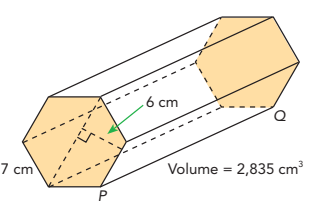
Janice is m aking a gift box. The gift box is a prism with bases that are regular hexagons, and has the dimensions shown in the diagram.

a) Find the height PQ of the prism.

b) Find the surface area of the prism.

Solution :

Area of hexagon = (1/2) x perimeter x Apothem

= (1/2) x 6(7) x 6

= 126 cm²

a)  Volume of figure = base area x height

126 x height = 2835

height = 2835/126

height = 22.5

b)  Surface area of prism = perimeter of the base x height

= 6(7) x 22.5

= 945 cm²

Problem 7 :

Container A was filled with water to the brim. Then, some of the water was poured into an empty Container B until the height of the water in both containers became the same. Find the new height of the water in both containers.

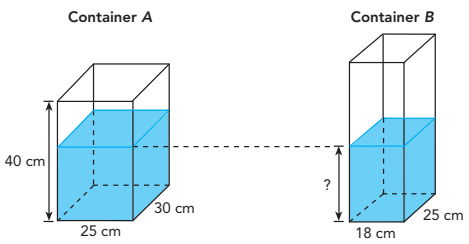
Solution :

Both containers are having equal quantity of water.

Quantity of water inside the container

= length x width x height

Let h be the new height of the container.

25 x 30 x 40 = 18 x 25 x h

h = (25 x 30 x 40)/(18 x 25)

h = 66.6 cm

Problem 8 :

A fish tank is 50 centimeters long, 30 centimeters wide, and 40 centimeters high. It contains water up to a height of 28 centimeters. How many more cubic centimeters of water are needed to fill the tank to a height of 35 centimeters?

Solution :

Length = 50 cm, width = 30 and height = 28

Capacity of water when its height is 28 cm :

= 50 x 30 x 28

= 42000 ----(1)

Length = 50 cm, width = 30 and height = 35

Capacity of water when its height is 35 cm :

= 50 x 30 x 35

= 52500 ----(2)

(2) - (1)

= 52500 - 42000

= 10500 cm³

Problem 9 :

Find the surface area of a square pyramid given that its base area is 196 square inches and the height of each of its triangular faces is 16 inches

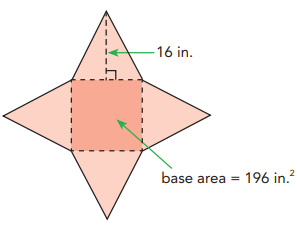
Solution :

Surface area of square base pyramid

= perimeter of the base x height

a² = 196

a = 14 in

Perimeter (4a) = 4(14)

= 56 inches

Height of the triangular face will be the height of square base prism.

Using Pythagorean theorem :

height of prism = √16² - 14²

= √256-196

= √60

Surface area = 56√60

= 56(7.74)

= 433.44

Problem 10 :

The volume of a rectangular prism is 441 cubic feet. It has a square base with edges that are 7 feet long.

a) Find the height of the prism.

b) Find the surface area of the prism

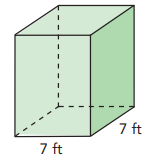
Solution :

a)  Volume of rectangular prism = base area x height

441 = 7 x 7 x h

h = 441/49

h = 9 ft

b) surface area = perimeter of base x height

= 4(7) x 9

= 252 ft²