STATE IN WHICH QUADRANT THE TERMINAL SIDE LIES

The angle is determined by rotating a ray about its endpoint. The starting position of the ray is initial side and the position after rotation is called  terminal side.

The endpoint of the ray are vertex of the angle.

Standard position :

An angle is said to be in standard position if its vertex is at the origin and its initial side is along the positive x-axis.

An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant.

Positive angles ang negative angles :

Positive angles are generated by counterclockwise rotation and negative angles are generated by clockwise rotation.

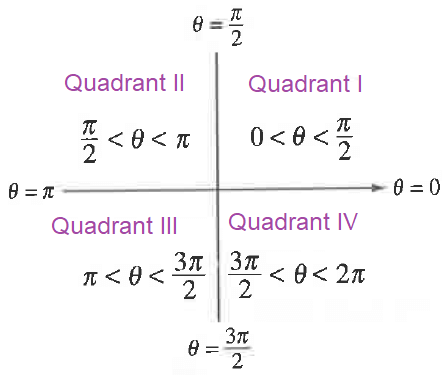
In angle measures :

0 < θ < 90 90 < θ <180 180 < θ < 270 270 < θ < 360

1st quadrant 2nd quadrant 3rd quadrant 4thquadrant

State the quadrant in which the terminal side of each angle lies

Problem 1 :

5π/6

Solution :

So, the given angle measure 5π/6 lies in 2^nd quadrant.

Problem 2 :

-7π/4

Solution :

By converting the radian measure to degree measure, we can easily find the terminal side lies in which quadrant.

The given angle lies in 1^st quadrant.

Problem 3 :

13π/9

Solution :

The given angle lies in 3^rd quadrant.

Problem 4 :

-17π/18

Solution :

The given angle lies in 2^nd quadrant.

Problem 5 :

330°

Solution :

The given angle lies between 270° to 360°. So, the given angle lies in 3^rd quadrant.

Problem 6 :

-25°

Solution :

The given angle lies between 0° to -90°. So, the given angle lies in 1^st quadrant.

Problem 7 :

-380°

Solution :

-380° = -360° - 20°

From this, we understand that the angle completes one complete revolution and having 20° more in the clockwise direction. So, the required angle lies in 1^st quadrant.

Problem 8 :

480°

Solution :

480° = 360° + 120°

= 360° + 90° + 30°

From this, we understand that the angle completes one complete revolution and having 120° more in the counter clockwise direction. So, the required angle lies in 2^nd quadrant.