STATE DOMAIN AND RANGE Y-INTERCEPT OF EXPONENTIAL FUNCTION

Graph each of the following and find the domain and range for each function.

Problem 1 :

f(x) = 2^x

Solution :

To graph the given function, by applying some of the random values of x. We get,

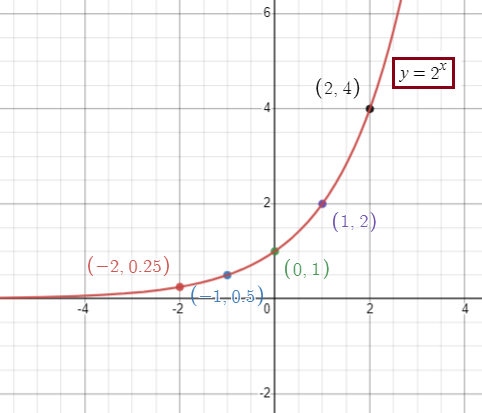
By observing  the graph,

The function is defined for all values of x. So, domain is 

(-∞, ∞)

The function is defined, for all positive values of y. So, the range is

(0, ∞)

Problem 2 :

f(x) = 2^x+5 - 5

Solution :

To graph the given function, by applying some of the random values of x. We get,

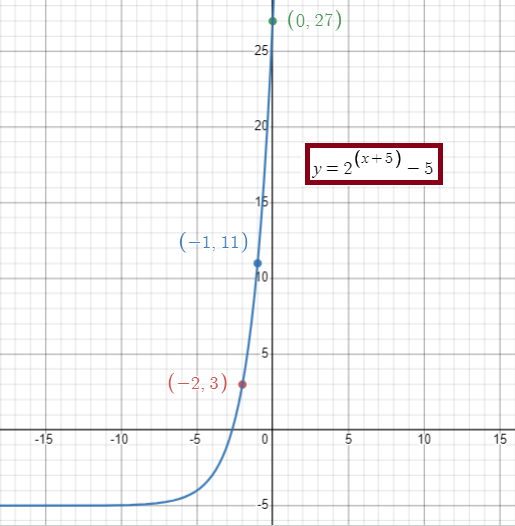
Horizontal asymptote :

y = -5

Domain = (-∞, ∞)

Range = (-5, ∞)

Problem 3 :

f(x) = 3^-x

Solution :

To graph the given function, by applying some of the random values of x. We get,

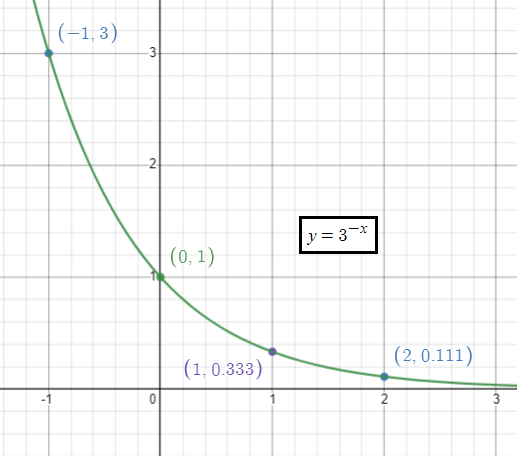
Horizontal asymptote :

y = 0

Domain = (-∞, ∞)

Range = (0, ∞)

Problem 4 :

f(x) = -2^-x

Solution :

To graph the given function, by applying some of the random values of x. We get,

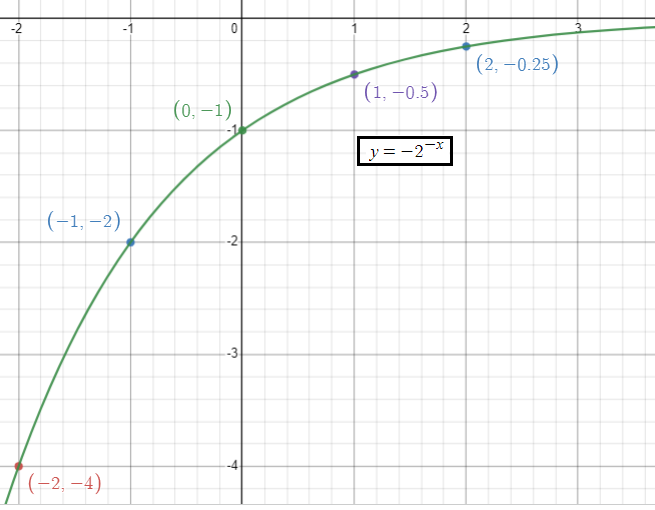
Horizontal asymptote :

y = 0

Domain = (-∞, ∞)

Range = (-∞, 0)

Problem 5 :

Sketch the graph of the function

y = 4 (2)^x

Solution :

y = 4 (2)^x

The given function is in the form of y = a(b)^x

Here a = 4 and b = 2

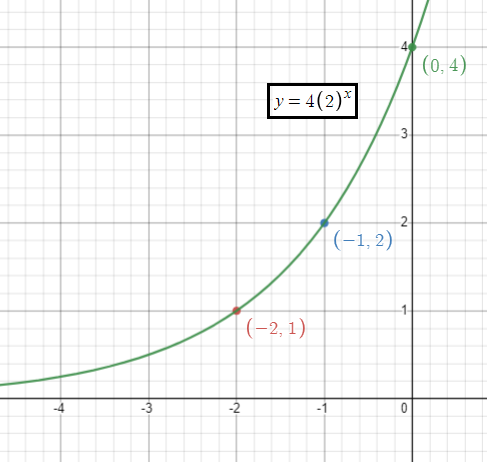
Horizontal asymptote :

y = 0

Domain = (-∞, ∞)

Range = (0, ∞)

Problem 6 :

Sketch the graph of the function

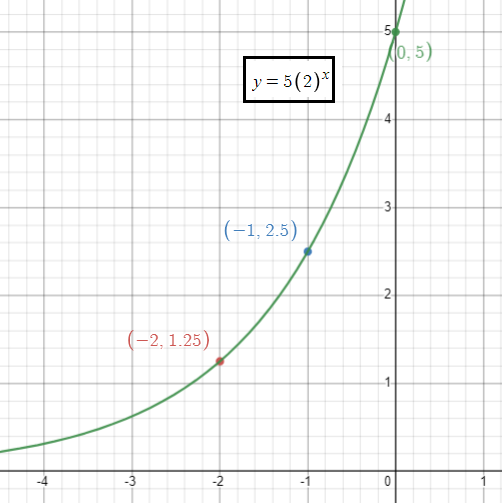
y = 5 (2)^x

Solution :

y = 5 (2)^x

The given function is in the form of y = a(b)^x

Here a = 5 and b = 2

Problem 7 :

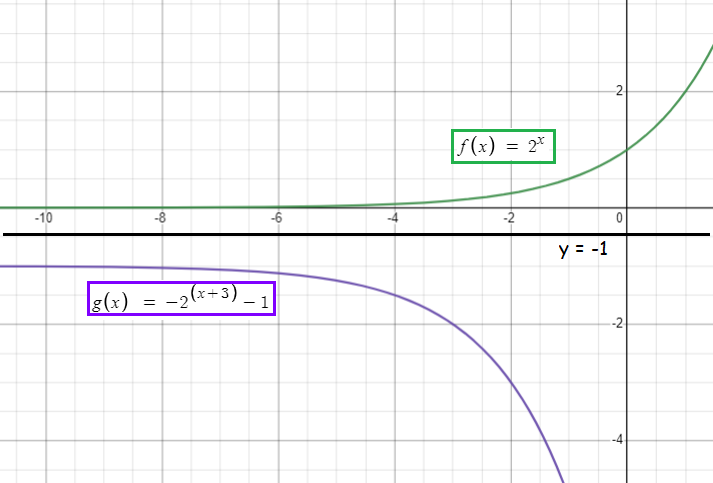
Use f(x) = 2^x to obtain the graph of g(x) = -2^x+3 - 1, find

i) Horizontal asymptote

ii)  Domain 

iii) Range

Solution :

Comparing f(x) = 2^x and g(x) = -2^x

It is a reflection across y-axis. 

Comparing the function g(x) with

= a(b^x+h) + k

a = 1, b = 2, h = -3 and k = -1

We move the graph 3 units to the left and move it down 1 unit.