STANDARD FORM TO VERTEX FORM
To convert standard form to vertex form, we may follow the different ways.
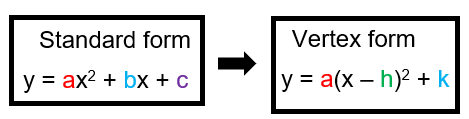
Completing the square method
From the standard form of the equation, y = ax2 + bx + c
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Write the coefficient of x as a multiple of 2.
(iii) Get any one of the algebraic identities (a+b)2 or (a-b)2
Example :
Convert the following quadratics from standard form to vertex form
y = 2x2 – 4x + 8
Solution :
y = 2x2 – 4x + 8
Factor 2.
y = 2(x2 – 2x + 4)
Write the coefficient of x as a multiple of 2.
y = 2(x2 – 2⋅x⋅1 + 12 - 12 + 4)
Here x2 – 2⋅x⋅1 + 12 matches with a2 – 2⋅a⋅b + b2 = (a - b)2
y = 2[(x - 1)2 - 1 + 4]
y = 2[(x - 1)2 + 3]
Distributing 2, we get
y = 2(x - 1)2 + 6
Using short cut
From the standard form of the equation, y = ax2 + bx + c
(i) Take the coefficient of x2, from all the terms if there is.
(ii) Take half of the coefficient of x and write it as (x - a)2 or (x + a)2. Here a is half the coefficient of x.
Example :
Convert y = x2 - 4x + 3 into factored form.
Solution :
y = x2 - 4x + 3
Coefficient of x2 is 1, so dont have to factor anything.
Half of the coefficient of x is 2.
y = (x - 2)2 - 22 + 3
y = (x - 2)2 - 4 + 3
y = (x - 2)2 - 1
More Examples
Complete the square to convert the standard form quadratic function into vertex form. Then
find the vertex.
Example 1 :
f(x) = x2 + 4x - 14
Solution :
Coefficient of x2 is 1. So, don't have to factorize.
Write the coefficient of x as multiple of 2.
f(x) = x2 + 2 ⋅ x ⋅ 2 + 22 - 22 - 14
f(x) = (x+2)2 - 4 - 14
f(x) = (x+2)2 - 18
Vertex of the parabola is (-2, -18).
Example 2 :
f(x) = 2x2 + 9x
Solution :
Coefficient of x2 is 2.
Write the coefficient of x as multiple of 2.
Vertex of the parabola is (9/4, -81/8).
Example 3 :
f(x) = 5x2 - 4x + 1
Solution :
Coefficient of x2 is 5. So, we have to factorize 5.
Vertex of the parabola is (2/5, 1/5).
Example 4 :
f(x) = x2 - 16x + 70
Solution :
Coefficient of x2 is 1. So, don't have to factorize.
Write the coefficient of x as multiple of 2.
f(x) = x2 - 2 ⋅ x ⋅ 8 + 82 - 82 + 70
f(x) = (x - 8)2 - 64 + 70
f(x) = (x - 8)2 + 6
Vertex of the parabola is (8, 6).
Example 5 :
f(x) = -3x2 + 48x - 187
Solution :
Coefficient of x2 is -3. So, factorize -3.
f(x) = -3[x2 - 16x] - 187
Write the coefficient of x as multiple of 2.
f(x) = -3[x2 - 2 ⋅ x ⋅ 8 + 82- 82] - 187
f(x) = -3[(x - 8)2- 64] - 187
f(x) = -3(x - 8)2+ 192 - 187
f(x) = -3(x - 8)2+ 5
Vertex of the parabola is (8, 5).
Related Pages
- Converting from standard into vertex form
- Converting from vertex form to standard form
- Examples on converting from standard form to factored form
- Converting from standard form to factored form worksheet
- Converting from Standard form to vertex form
- Converting from standard form to vertex form worksheet
- Converting from standard form to factored form
- Converting between different forms of quadratic functions worksheet
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling