STAAR TEST ALGEBRA 1 PRACTICE TEST WITH SOLUTIONS

Problem 1 :

Which expression is equivalent to (5rt - 3rw - 8tw) + (6rt - 4rw + 2tw) ?

A) 11rt + rw - 10tw      B) 11rt - 7rw - 6tw     C) 11rt + rw - 6tw

D) 11rt - 7rw - 10tw

Solution :

5rt - 3rw - 8tw + 6rt - 4rw + 2tw

11rt - 7rw - 6tw

So, option B) is correct.

Problem 2 :

The solutions to p(x) = 0 are x = -7 and x = 7. Which quadratic function could represent p ?

F) p(x) = x² - 49     G) p(x) = x² + 49    H) p(x) = x² - 14

J) p(x) = x² + 14

Solution :

x = -7 and x = 7

(x + 7) (x - 7)

x² - 7x + 7x - 7²

x² - 49

So, option F) is correct.

Problem 3 :

Two points are plotted on the grid.

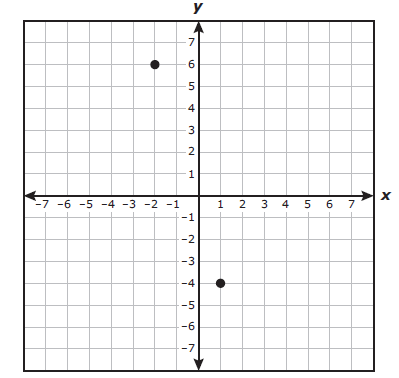
Which equation in slope - imtercept form best represents the line that passes through these two points ?

Solution :

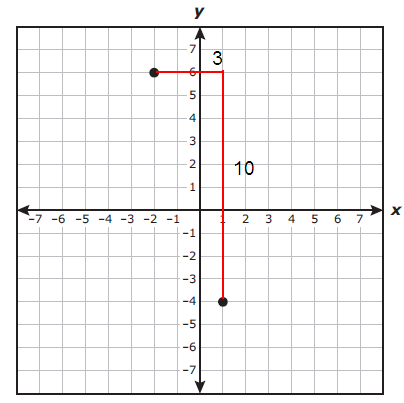
Slope (m) = -10/3

y = mx + b

y = -(10/3)x + b

Passes through these two points = (-2, 6) and (1, -4).

6 = -(10/3) × (-2) + b

6 = 20/3 + b

6 - 20/3 = b

18/3 - 20/3 = b

-2/3 = b

-4 = -(10/3) × 1 + b

-4 = -10/3 + b

-4 + 10/3 = b

-12/3 + 10/3 = b

-2/3 = b

y = -(10/3)x - 2/3

So, option D) is correct.

Problem 4 :

The table shows the value in dollars of a motorcycle at the end of x years.

Motorcycle

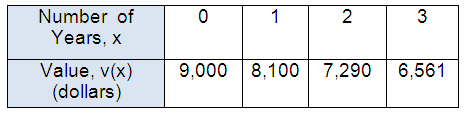
Which exponential function models this situation ?

F) v(x) = 9,000(1.1)^x           G) v(x) = 9,000(0.9)^x

H) v(x) = 8,100(1.1)^x           J) v(x) = 8,100(0.9)^x

Solution :

Exponential function will be in the form y = ab^x

when x = 0 and y = 9000

Applying this in the above function, we will get a = 9000

Applying one more point say (1, 8100)

8100 = 9000 × b¹

8100 = 9000 × b

8100/9000 = b

b = 0.9

So,  the value of b is 0.9.

y = 9000 × 0.9^x

Let y = v(x)

v(x) = 9000 × 0.9^x

So, option G) is correct.

Problem 5 :

What is the positive solution to x² + 9x - 22 = 0 ?

Record your answer and fill in the bubbles on your answer document.

Solution :

Given, x² + 9x - 22 = 0

x² + 11x - 2x - 22 = 0

x(x + 11) - 2(x + 11) = 0

(x - 2) (x + 11) = 0

x - 2 = 0 and x + 11 = 0

x = 2 and x = -11

So, the positive solution is x = 2.

Problem 6 :

A university will spend at most $4,500 to buy monitors and keyboards for a computer lab. Each monitor will cost $250, and each keyboard will cost $50.

Which inequality represents all possible combinations of x, the number of monitors, and y, the number of keyboards, the university can buy for the computer lab ?

F) 250x + 50y < 4,500           G) 250x + 50y ≤ 4,500

H) 50x + 250y < 4,500           J) 50x + 250y ≤ 4,500

Solution :

Amount spent by University = $4500

The cost of each monitor = $250

The number of monitor = x

monitor = $250 × x

= $250x

The cost of each keyboard = $50

The number of keyboard = y

keyboard = $50 × y

= $50y

The maximum amount the university can spend is $4500.

$250x + $50y ≤ $4500.

So, option G) is correct.

Problem 7 :

A construction manager is monitoring the progress of the build of a new house. The scatterplot and table show the number of months since the start of the build and the percentage of the house still left to build. A linear function can be used to model this relationship.   

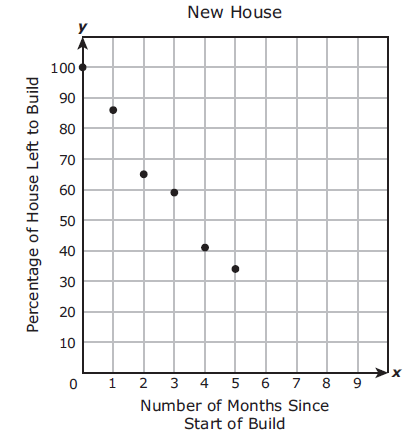
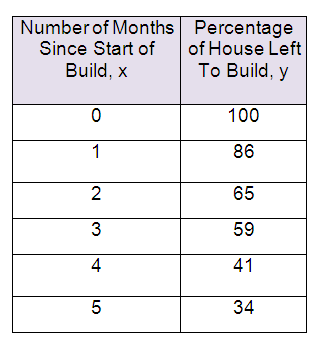
Which function best models the data ?

A) y = -13.5x + 97.8       B) y = -13.5x + 7.3

C) y = 97.8x - 13.5         D) y = 7.3x - 97.8

Solution :

Taking two points from the table 

(0, 100) and (1, 86)

m = (86 - 100) / (1 - 0)

m = -14

y-intercept is 100.

y = -14x + 100

Accordingly options given, A is very closer to the calculation. So, option A is correct.

Problem 8 :

Given f(x) = x² - 36, which statement is true ?

F) The only zero, 6, can be found when 0 = (x - 6) (x - 6).

G) The only zero, 18, can be found when 0 = (x - 18) (x - 18).

H) The zeros, -6 and 6, can be found when 0 = (x + 6) (x - 6).

J) The zeros, -18 and 18, can be found when 0 = (x + 18) (x - 18).

Solution :

Given f(x) = x² - 36

= x² - 6²

= (x + 6) (x - 6)

x + 6 = 0 and x - 6 = 0

x = -6 and x = 6

The zeros, -6 and 6, can be found when 0 = (x + 6) (x - 6).

So, option H) is correct.

Problem 9 :

A function is shown.

f(x) = 7 - 4x

What is the value of f(-5) ?

A) 27           B) -13          C) -15              D) 140

Solution :

Given, f(x) = 7 - 4x

f(-5) = 7 - 4(-5)

= 7 + 20

f(-5) = 27

So, option A) is correct.

Problem 10 :

Which graph best represents y = -4(x + 3) - 2 ?

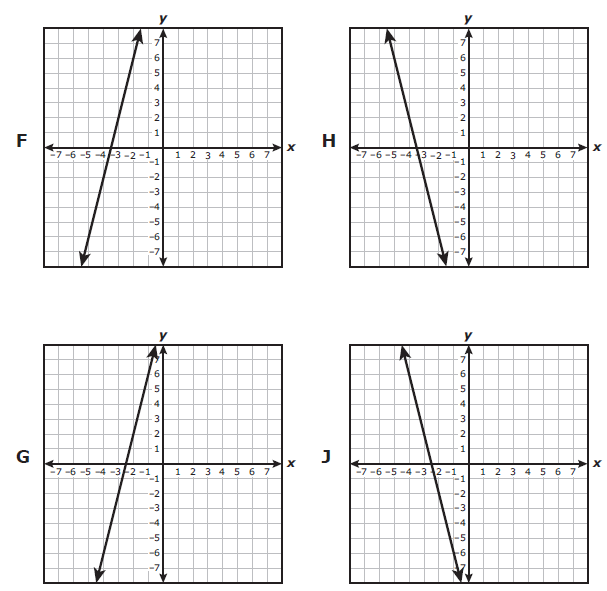
Solution :

Given, y = -4(x + 3) - 2

y = -4x - 12 - 2

y = -4x - 14

Compare y = -4x - 14 is equal to y = mx + b

m = -4, b = -14 and y = 0

0 = -4x - 14

-4x = 14

x = -14/4

x = -7/2

x intercepts is (-7/2, 0).

In both option F and H, x-intercept is -3.5 only, since we have negative slope it must be a falling line. So, option H is correct.