SQUARE ROOT OF DECIMALS WITHOUT CALCULATOR

Find :

Problem 1:

√0.01

Solution :

= √0.01

After the decimal, we have two digits. So multiply the numerator and denominator by 100.

= √1/100

= √1/√100

= 1/10

= 0.1

Problem 2 :

√0.25

Solution :

= √0.25

After the decimal, we have two digits. So multiply the numerator and denominator by 100.

= √(25/100)

= √25/√100

= √(5⋅5)/√(10⋅10)

= 5/10

= 0.5

Problem 3 :

√0.81

Solution :

= √0.81

= √81/100

= √81/√100

= √(9⋅9)/√(10⋅10)

= 9/10

= 0.9

Problem 4 :

√0.6889

Solution :

= √0.6889

= √6889/10000

= √6889/√10000

Since the unit digit is 9 and starts with 68.

83 x 83 = 6889

87 x 87 = 7569

= 83/100

= 0.83

Problem 5 :

√0.7921

Solution :

= √0.7921

= √7921/10000

= √7921/√10000

Since the unit digit is 1 and starts with 79.

87 x 87 = 7569

89 x 89 = 7921

= 89/100

= 0.89

Problem 6 :

√0.9025

Solution :

= √0.9025

= √9025/10000

= √9025/√10000

Since the unit digit is 5 and starts with 90.

85 x 85 = 7225

95 x 95 = 9025

= 95/100

= 0.95

Problem 7 :

√48.8601

Solution :

= √48.8601

= √488601/10000

= √488601/√10000

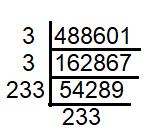
= 699/100

= 6.99

Square Root Using Long Division

Simplify the square roots.

Problem 1 :

√35.88

Solution :

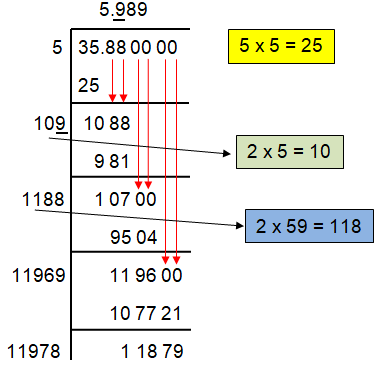
So, the square root of 35.88 is 5.989.

Problem 2 :

√36.46

Solution :

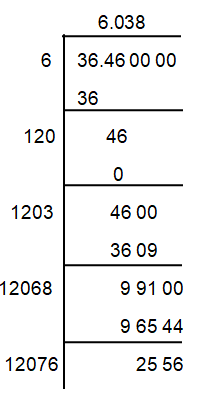
So, the square root of 36.46 is 6.038.

Problem 3 :

√89.87

Solution :

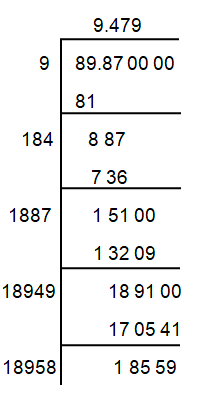
So, the square root of 89.87 is 9.479.

Problem 4 :

√99.80

Solution :

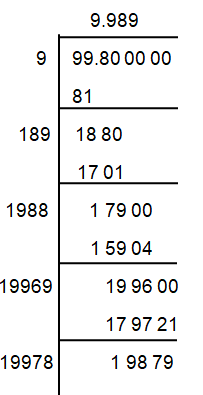
So, the square root of 99.80 is 9.989.

Problem 5 :

√62.25

Solution :

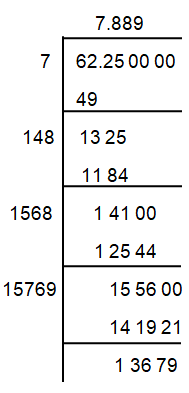
So, the square root of 62.25 is 7.889.

Problem 6 :

√97.81

Solution :

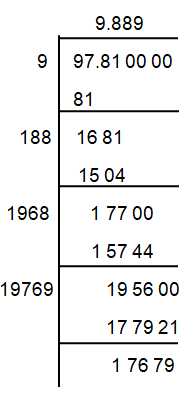
So, the square root of 97.81 is 9.889.