SOLVING WORD PROBLEMS WITH VENN DIAGRAM OF 2 CIRCLES

Problem 1 :

In a group of 100 children, 62 like pizza, 47 like burger and 36 like both. Find the number of students who like pizza but not burger.

a) 26     b) 15      c) 36      d) 30

Solution :

Total number of children = 100

Number of children who like pizza = 62

Number of children who like burger = 47

Number of children who like both = 36

Representing the given details in venn diagram,

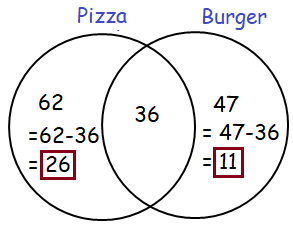
Number of children who like pizza = 26

So, option a is correct.

Problem 2 :

In a group of 50 persons, everyone takes either tea or coffee. If 35 take tea and 25 take coffee, then the number of persons who take tea only (and not coffee) is

a) 10       b) 25       c) 35        d) 30

Solution :

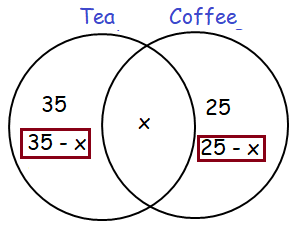
Total number of persons = 50

All 50, they used to drink any of the above.

35 - x + x + 25 - x = 50

60 - x = 50

x = 60 - 50

x = 10

Number of persons who like tea only :

= 35 - x

Applying the value of x,

= 35 - 10

= 25

So, the number of persons who like tea only not coffee is 25.

Problem 3 :

25 people for programme A, 50 people for progamme B, 10 people for both. So, the number of employee employed only for programme A are

a) 15    b) 20     c) 35      d) 40

Solution :

Number of people for programme A = 25

Number of people for programme B = 50

Number of people who are in both = 10

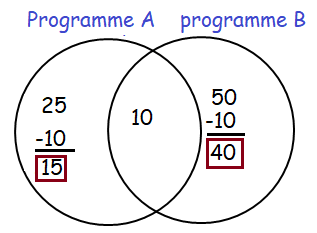
So, the number of  employee employed only for programme A are 15.

Problem 4 :

A PE test has two sections, theory and practical. Everyone in a class who took the PE test passed at least one section. 62% passes the theory section and 83% passed the practical section.

(a) Represent this information on a Venn diagram

(b) the number of person who passed the theory section, given they passed the practical section. 

(c) passed the practical section, given they passed only one section

Solution :

a)

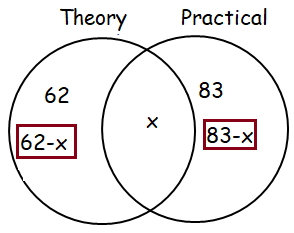
b) Solving for x :

62 - x + x + 83 - x = 100

145 - x = 100

-x = 100 - 145

x = 45

c) Number of students who passed in theory section :

= 62 - 45

= 17

Number of students who passed in practical section :

= 83 - 45

= 38

Problem 5 :

In a class of 60 students, 25 students play cricket and 20 students play tennis and 10 students play both the games, then the number of students who play neither is

a) 45      b) 0       c) 25        d) 35

Solution :

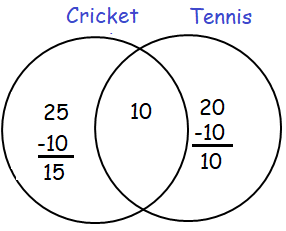
Total number students = 60

Number of students who plays atleast one game

= 15 + 10 + 10

= 35

Number of students who play neither = 60 - 35

= 25

Problem 6 :

Sets A and B are such that A has 25 members, B has 20 members and A U B has 35 members. The number of members in the set A n B is

a) 10      b) 5        c) 15        d) 20

Solution :

n(A) = 25

n(B) = 20

n(AUB) = 35

n(AnB) = n(A) + n(B) - n(AnB)

= 25 + 20 - 35

= 45 - 35

n(AnB) = 10

Problem 7 :

In a class of 100 students, 60 play cricket, 50 play volleyball and 28 play both. Find the number of students who play atleast one of the two games.

a) 18       b) 32       c) 110        d) 82

Solution :

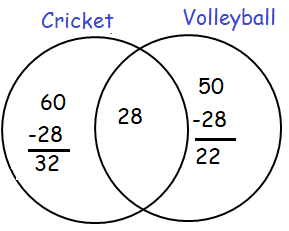
Number of students who play atleast one of the two games = 

= 32 + 25 + 22

= 82

So, the number of students who play atleast one of the game is 82.

Problem 8 :

If X is the universal set and A, B are subsets of X such that n(X) = 99, n(A') = 80, n(B') = 85 and n(A n B)' = 94, then n(A U B) =

a) 33      b) 14      c) 28     d) 29

Solution :

n(X) = 99, n(A') = 80, n(B') = 85 and n(A n B)' = 94

To find n(AUB), let us use the formula

n(A U B) = n(A) + n(B) - n(AnB)

n (A) = n(X) - n(A')

n (B) = n(X) - n(B')

n (A) = 99 - 80 ==> 19

n (B) = 99 - 85 ==> 14

n(AnB) = n(X) - n(AnB)'

n(AnB) = 99 - 94 ==> 5

n(A U B) = 19 + 14 - 5

= 28

So, the answer is 28.

Problem 9 :

In a consumer - preference survey of an item, fifteen were found to use Brand A, twenty were found to use Brand B, five were found to be in the habit of using both brands A and B. Find the number of consumers using at least one of the two brands of the item.

a) 30     b) 20     c) 15         d) 35

Solution :

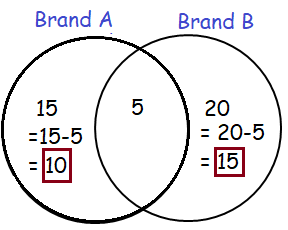
The number of customers who use atleast one of the brands

= 10 + 5 + 15

= 30

So, the answer is 30.