SOLVING WORD PROBLEMS WITH RECTANGULAR PRISMS

In geometry, a rectangular prism can be defined as a 3-dimensional solid shape which has six faces that are rectangles. A rectangular prism is also a cuboid.

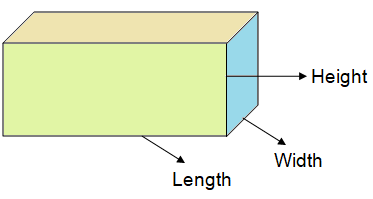
Lateral surface area = 2h(l + w)

Total surface area = 2(lw + wh + hl)

Volume = length x width x height

Problem 1:

The lateral surface area of a cuboid whose length, width  and height are 2a, 2b and 2c respectively is

a)  2(ab + bc + ca)    b)  4(ab + bc + ca)

c)  8(a + b) c     d)  none of these

Solution :

Lateral surface area = 2h(l + b)

= 2(2c) (2a + 2b)

= 8c(a + b)

So, option (c) is correct.

Problem 2 :

The sum of the areas of all faces (excluding top and bottom) of a cuboid is the ___________ of the cuboid.

a) Volume      b) lateral surface area

c) Total surface area     d) none of these

Solution :

The sum of the areas of all faces (excluding top and bottom) of a cuboid is the lateral surface area of the cuboid.

So, option (b) is correct.

Problem 3 :

The volume of a cuboid whose length, breadth and height are 2a, 3a and 4a is

a)  24a²    b)  24a³     c) 12a³     d) none of these

Solution :

Length = 2a, width = 3a and Height = 4a

Volume of the cuboid = length × width × height

V = 2a × 3a × 4a

V = 24a³

So, option (b) is correct.

Problem 4 :

Find the height of a cuboid whose volume is 756 cm³ and base area is 63 cm²?

Solution :

Volume of the cuboid = 756 cm³

Base area = 63 cm²

Volume of the cuboid = length × breadth × height

756 = base area × h

h = 756/63

h = 12 cm

So, height of the cuboid is 12 cm.

Problem 5 :

The dimension of a cuboid are in the ratio of 2:3:4 and its total surface area is 280 m². Find the dimensions.

Solution :

Total surface area = 280 m²

Total surface area = 2(lb + bh + lh)

280 = 2[(2x · 3x) + (3x · 4x) + (2x · 4x)]

280 = 2(6x² + 12x² + 8x²)

280 = 2(26x²)

280 = 52x²

x² = 280/52

x² = 5.3

x = √5.3

x = 2.3

Therefore, length = 2x = 2 · 2.3 = 4.6 m

Breadth = 3x = 3 · 2.3 = 6.9 m

Height = 4x = 4 · 2.3 = 9.2 m

Problem 6 :

A cuboid is 40 cm × 20 cm × 10 cm. what would be the side of a cube having the same volume?

a) 20cm     b) 40cm    c) 10cm    d) 30cm

Solution :

Length = 40 cm, width = 20 cm and Height = 10 cm

Volume of cuboid = length × breadth × height

= 40 × 20 × 10

= 8000 cm³

Then, side of a cube a³ = 8000

a³ = (20)³

a = 20 cm

So, option (a) is correct.

Problem 7 :

A cuboid has a volume of 3000 cm³, with height 15 cm and length 20 cm. Find the area of the upper surface.

Solution :

Volume of cuboid = 3000 cm³

Length = 20 cm and Height = 15 cm

Volume of cuboid = length × breadth × height

3000 = 20 × breadth ×15

3000 = 300 × breadth

Breadth = 3000/300

= 10 cm

Area of upper surface = length × breadth

= 20 × 10

= 200 cm²

So, area of the upper surface is 200 cm².

Problem 8 :

The sum of length, breadth and depth of a cuboid is 19 cm and the diagonal is 5√5. Find its surface area.

Solution :

Given, l + b + h = 19 cm

Diagonal = 5√5

√ (l² + b² + h²) = 5√5

l² + b² + h² = (5√5)²

= 125 cm

Surface area of the cuboid = 2(lb + bh + lh)

= (l + b + h)² - (l² + b² + h²)

= 19² - 125

= 361 - 125

= 236 cm²

So, surface area of cuboid is 236 cm².

Problem 9 :

Three cubes with sides in the ratio 3:4:5 are melted to form a single cube whose diagonal is 12√3 cm. find the sides of the cube.

Solution :

Let edge of first cube = 3x, Edge of 2^nd cube = 4x and 

Edge of third cube = 5x

Volume of new cube formed = (3x)³ + (4x)³ + (5x)³

= 27x³ + 64x³ + 125x³

= 216 x³

Diagonal of a cube = √3 a

√3 a = 12√3

a = 12 cm

Volume of new cube = (12)³

(12)³ = 216x³

x³ = 1728/216

x³ = 8

x = 2

Therefore, side of first cube = 3 × 2 = 6 cm

Side of second cube = 4 × 2 = 8 cm

Side of third cube = 5 × 2 = 10 cm