SOLVING WORD PROBLEMS WITH 3 CIRCLES

Problem 1 :

A group of 30 students are surveyed to find out which of the three sports, soccer (S), basketball (B) or volleyball (V), they play. The results are as follows :

(i) 3 children do not play any of these sports

(ii) 2 children play all three sports

(iii) 6 play volleyball and basketball

(iv) 3 play soccer and basketball

(v) 6 play soccer and volleyball

(vi) 16 play basketball

(vii) 12 play volleyball

(A) Draw a Venn Diagram representing this situation.

(B) How many students play soccer only ?

(C) How many students play soccer but not basketball ?

(D) How many students play volleyball but not basketball ?

Solution :

(A) Let x be the student play soccer.

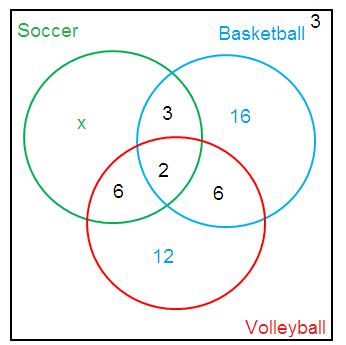
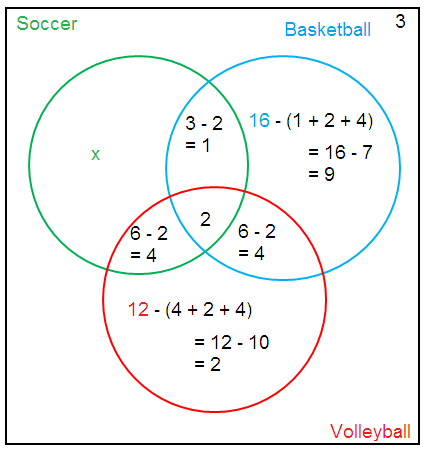
(B) 

x + 1 +  9 + 4 + 2 + 4 + 2 + 3 = 30

x + 25 = 30

x = 30 - 25

x = 5

So, 5 student play soccer only.

(C) 

n(S) = 5

n(S ∩ B) = 4

= 5 + 4

= 9

So, 9 students play soccer.

(D) 

4 + 2 = 6

So, 6 students play volleyball. 

Problem 2 :

There are 36 students who study science. 14 study physics, 18 study chemistry, 24 study Biology, 5 study physics and chemistry, 8 study physics and biology, 10 study biology and chemistry, 3 study all three subjects.

(A) Create Venn Diagram of the situation.

(B) Determine the number of students who study Physics and Biology only.

(C) Determine the number of students who study at least two subjects.

(D) Determine the number of students who study biology only.

Solution :

A)

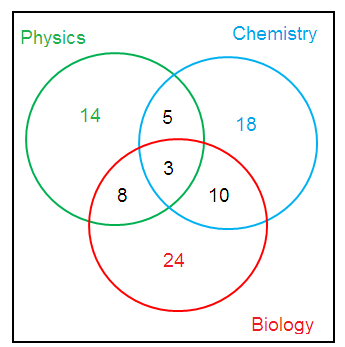
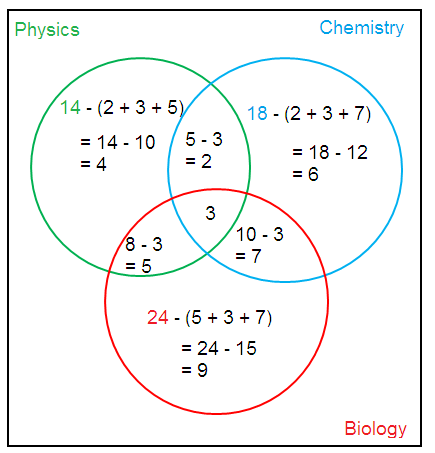
B) 5 students study Physics and Biology only.

C) number of students who study at least two subjects

= 2 + 3 + 5 + 7

= 17

D) Number of students who study biology only = 9

Problem 3 :

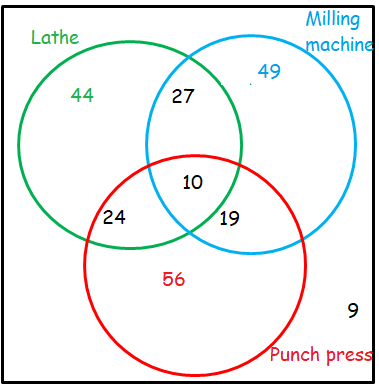
A survey of a machine shop reveals the following information about its employees :

44 employees can run a lathe, 49 employees can run the milling machine, 56 employees can operate a punch press, 27 employees can run a lathe and a milling machine, 19 employees can run a milling machine and operate a punch press, 24 employees can run a lathe and operate a press punch, 10 employees can operate all three machines, 9 employees cannot operate any of the three machines.

Draw a Venn Diagram and use it to determine the number of employed at the machine shop.

Solution :

Representing the given information in Venn diagram :

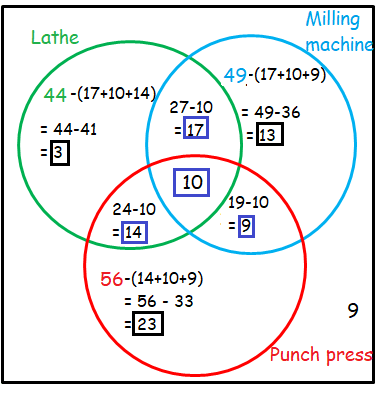
Number of employee in the shop

= 3 + 17 + 13 + 14 + 10 + 9 + 23 + 9

= 98

So, 98 employed at the machine shop.

Problem 4 :

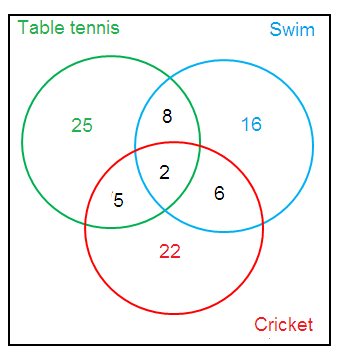
In a group of 60 students :

2 students play all three

8 play table tennis and swim

6 play cricket and swim

5 play table tennis and cricket

25 play table tennis

16 swim

22 play cricket

a) Create a Venn diagram to model the information.

b) How many play table tennis and swim and play cricket ?

c) How many play table tennis but not cricket ?

d) How many play table tennis and cricket but not do swimming ?

Solution :

a)

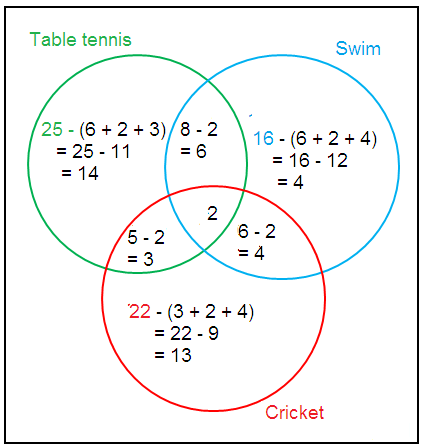
b) 

= 14 + 13 + 4 + 3 + 4 + 6

= 44

So, 44 students table tennis and swim and play cricket.

c)

n(T ∩ C) = 3

n(T) = 14

= 14 - 3

= 11

So, 11 students play table tennis but not cricket.

d)

= 14 + 4 + 13

= 31

Hence 31 students table tennis and swim and play cricket.

Problem 5 :

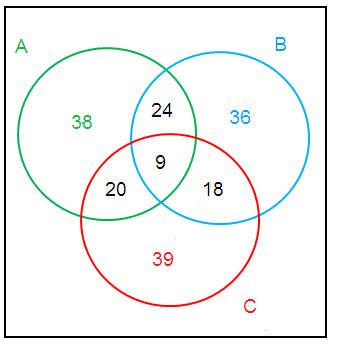
9 liked all the three products

24 people liked both products A and B

20 people liked products C and A

18 people liked products B and C

38 people liked products A 

36 liked product B

39 liked product C

a) Create a Venn diagram to model the information.

b) How many liked product A or B ?

c) How many liked product both A and B, but not C ?

d) How many didn't like any of the three products ?

Solution :

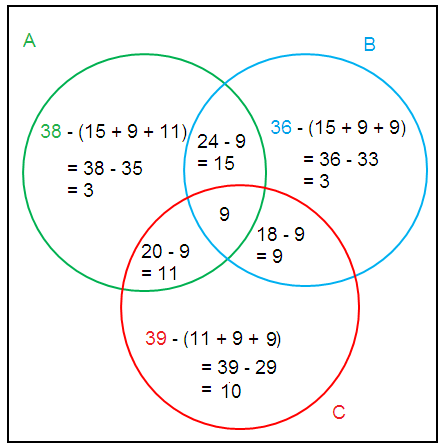
a) Representing in the venn diagram :

b) Number of people who liked product A or B 

= 3 + 11 + 9  + 15 + 9 + 3

= 50

c) Number of people who liked product both A and B, but not C 

= 15

d) How many didn't like any of the three products 

= 15