SOLVING WORD PROBLEMS USING PYTHAGOREAN THEOREM

Problem 1 :

A land surveyor uses this diagram to find x, find the length of lake.

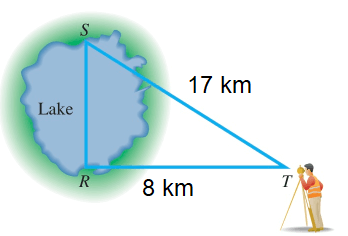
Solution :

Using Pythagorean theorem,

ST² = SR² + RT²

17² = SR² + 8²

289 = SR² + 64

289 - 64 = SR²

SR² = 225

SR = √225

SR = 15

Problem 2 :

A foot ladder leans against a shed reaching a height of x feet. The base of the ladder is 10 feet from the shed.

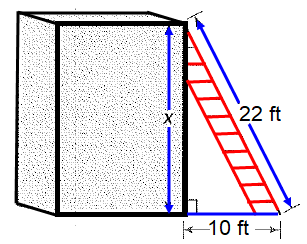
Solution :

Using Pythagorean theorem, 

22² = x² + 10²

484 = x² + 100

x² = 484 - 100

x² = 384

x = √384

x = 19.59 ft

Problem 3 :

The diagram shows a sailboat. What is approximate area of the sail shown ?

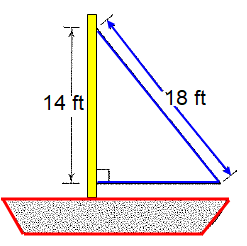
(a)  79 square feet     (b)  126 square feet

(c)  158 square feet      (d)  200 square feet

Solution :

We use Pythagorean theorem to find the missing side. Let the missing side be x.

18² = x² + 14²

324 = x² + 196

x² = 324 - 196

x² = 128

x = √128

x = 11.31

Area of the boat = (1/2) x base x height

= (1/2) x 11.31 x 14

= 7 x 11.31

= 79.17 square feet

So, the required area is 79 square feet.

Problem 4 :

The television screen has a 25 inch diagonal and a 15 inch height. What is the area of the screen ?

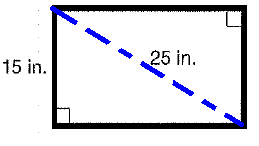
(a)  150 square inches    (b)  300 square inches

(c)  375 square inches   (d) 437 square inches

Solution :

Let x be the length of the screen.

x² + 15² = 25²

x² + 225 = 625

x² = 625 - 225

x² = 400

x = 20

Area of the screen = length (width)

= 20 (15)

= 300 square inches

Problem 5 :

If two forces, A and B pull at right angles from each other, the resultant force can be represented as the diagonal of a rectangle.

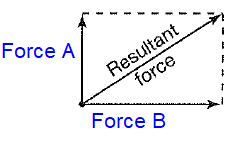
If a 21 pound force and a 28 pound force are pulling of an object, and the resultant force is 35 pounds, are the forces pulling a right angles ?

Solution :

21² + 28² = 35²

441 + 784 = 1225

1225 = 1225

Yes the forces are pulling at right angle.

Problem 6 :

The distance across a pond cannot be directly measured. A land surveyor takes some other measurements and uses them to find d, the distance across the pond.

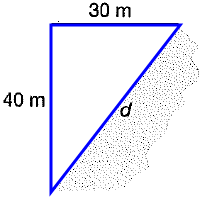
What is the distance across the pond ?

(a)  70 meters   (b) 35 meters   (c)  50 meters    (d) 10 meters

Solution :

30² + 40² = d²

900 + 1600 = d²

d² = 2500

d = √2500

d = 50

Problem 7 :

The solid line below show the route Maddy's bus takes to school. The dashed line shows a shortcut she takes through the park when she rides her bike to school. What is the difference in km between the shortcut and the usual route ?

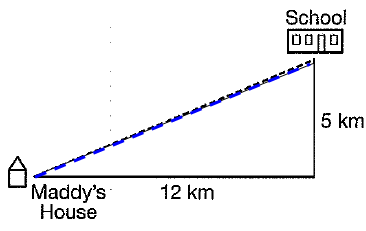
(a)  10 km     (b)  4 km     (c)  7 km    (d)  3 km

Solution :

Let x be the length of the dashed line (short cut)

12² + 5² = x²

144 + 25 = x²

x² = 169

x = √169

x = 13

Usual distance = 12 + 5 ==> 17 km

Difference = 17 - 13

= 4 km

Problem 8 :

On the map below, the post office is at origin (0, 0) and each unit represents 1 km. Amy lives 6 km east and 8 km north of the post office. if she rides her bike directly from her house to the post office, how far will she ride her bike ?

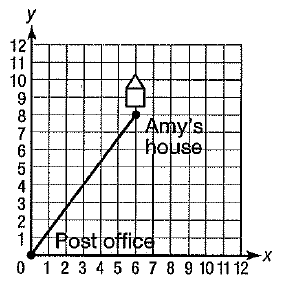
(a)  4.8 km   (b)  12 km   (c)  10 km   (d)  14 km

Solution :

Horizontal distance = 6 km

Vertical distance = 8 km

Distance between Post office to Amy's house = √8² + 6²

= √64 + 36

= √100

= 10

She will ride for 10 km.