SOLVING WORD PROBLMS ON PYTHAGOREAN THEOREM

Problem 1 :

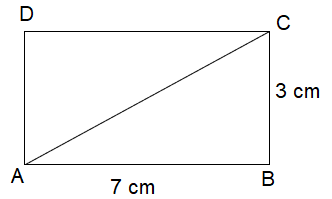
A rectangle has sides of length 7 cm and 3 cm. Find the length of its diagonals.

Solution :

In a rectangle, the diagonal will divide the rectangle into two right triangles.

x² = 900/10

AC² = AB² + BC²

AC² = 7² + 3²

AC² = 49 + 9

AC² = 58

AC = √58

AC = 7.61 cm

Problem 2 :

The longer side of the rectangle is double the length of the shorter side. If the length of a diagonal is 10 cm, find the dimension of the rectangle.

Solution :

Let x be the length of the shorter side.

Longer side = 2x

In rectangle, the diagonal side is hypotenuse.

So,

10² = x² + (2x)²

100 = x² + 4x²

5x² = 100

x² = 100/5

x² = 20

x = 2√5 cm

Longer side = 2(2√5) ==>  4√5 cm

Problem 3 :

A rectangle with diagonals of length 30 cm has sides in the ratio 3 : 1. Find the 

(a) Perimeter   (b) Area of the rectangle.

Solution :

Let "3x" and "x" be the length and width of the rectangle respectively.

Using Pythagorean theorem.

30² = (3x)² + x²

900 = 9x² + x²

900 = 10x²

x² = 900/10

x² = 90

x = √90

x = 3√10 (width)

3x = 3(3√10) ==>  9√10 (Length)

(a) Perimeter = 2(length + width)

= 2(9√10 + 3√10)

= 2 (12√10)

= 24√10 cm

(b) Area of the rectangle = length x width

= 9√10 x 3√10

= 27 (10)

= 270 cm²

Problem 4 :

A rhombus has sides of length 7 cm. One of the diagonals is 10 cm long. Find the length of the other diagonal.

Solution :

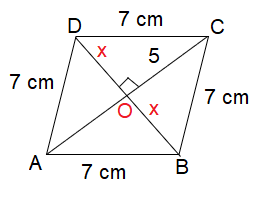
In rhombus, diagonals will bisect each other at right angle.

Triangle DOC

DC² = DO² + OC²

7² = x² + 5²

49 = x² + 25

49 - 25 = x²

x² = 24

x = 2√6

Length of other diagonal = 2x ==> 2(2√6)  ==> 12√6 cm

Problem 5 :

A square has diagonals of length 8 cm. Find the length of the sides.

Solution :

Let x be the side length of the square.

x² + x² = 8²

2x² = 64

x² = 32

x = √32

x = 4√2

So, side length of the square is 4√2.

Problem 6 :

A rhombus has diagonal of length 4 cm and 6 cm. Find the perimeter.

Solution :

In any rhombus, the diagonals will bisect each other at right angle.

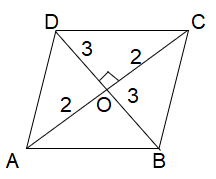
In triangle DOC

DC² = DO² + OC²

DC² = 3² + 2²

DC² = 9 + 4

DC² = 13

DC = √13

Perimeter of rhombus = 4√13.

Problem 7 :

An equilateral triangle has sides of 6 cm

(a)  Find the length one of its altitude.

(b)  Find the area of the triangle.

Solution :

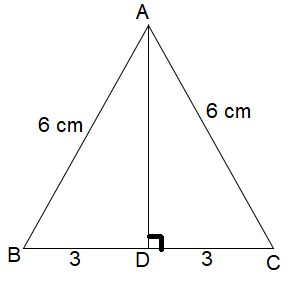
(a) Using Pythagorean theorem :

AC² = AD² + DC²

6² = AD² + 3²

36 - 9 = AD²

AD² = 27

AD = 3√3

(b)  Area of the triangle = (1/2) x base x height

= (1/2) x BC x AD

= (1/2) x 6 x 3√3

= 9√3

Problem 8 :

An isosceles triangle has equal sides of length 8 cm and the base of length 6 cm.

(a)  Find the altitude of the triangle

(b)  Find the area of the triangle

Solution :

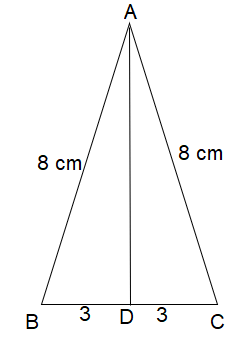
(a) Using Pythagorean theorem :

AC² = AD² + DC²

8² = AD² + 3²

64 - 9 = AD²

AD² = 55

AD = √55

(b)  Area of the triangle = (1/2) x base x height

= (1/2) x BC x AD

= (1/2) x 8 x √55

= 4√55 cm²