SOLVING WORD PROBLEMS ON CUBE AND CUBOID

Problem 1 :

Both cuboids below have the same volume. Find the height of cuboid B.

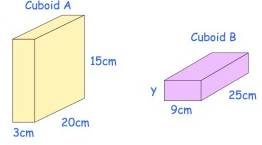
Solution :

Volume of a cuboid = (length × breadth × height) cubic units

20 × 3 × 15 = 25 × 9 × h

900 = 225 × h

h = 900/225

h = 4

So, the height of cuboid B is 4 cm.

Problem 2 :

The volume of the cube is twice the volume of the cuboid. Find the length of the cuboid.

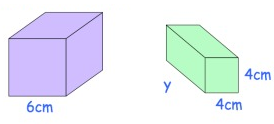
Solution :

Volume of a cube = (side)³

= 6³

= 216

Volume of a cuboid = (length × breadth × height) cubic units

Volume of a cuboid = y × 4 × 4

Volume of a cuboid = 16y

The volume of the cube is twice the volume of the cuboid.

So, 

Volume of a cube = 2 × Volume of a cuboid

216 = 2 × 16y

216 = 32y

y = 216/32

y = 6.75

So, the length of the cuboid is 6.75 cm.

Problem 3 :

The cuboid container below is used to store boxes. Each box is a cube with side length 1m. How many boxes can be stored in the container ?

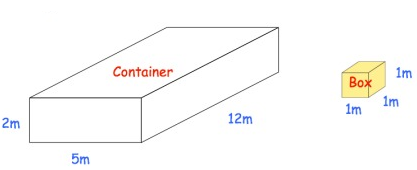
Solution :

Volume of a cube = (side)³

= 1³

Volume of a cube = 1

Volume of a cuboid = (length × breadth × height) cubic units

Volume of a cuboid = 5 × 12 × 2

Volume of a cuboid = 120

So, 120 boxes can be stored in the container boxes.

Problem 4 :

The volume of a cuboid is 15000 cm³. If the length is 30 cm and the width is 25 cm, find the height of the cuboid.

Solution :

Volume of a cuboid = (length × breadth × height) cubic units

volume of a cuboid = 15000 cm³

length of cuboid = 30 cm

width of cuboid =  25 cm

height of the cuboid = ?

15000 = 30 × 25 × h

15000 = 750h

h = 15000/750

h = 20

So, the height of the cuboid is 20 cm.

Problem 5 :

Shown is a net of a cuboid. Calculate the volume of the cuboid

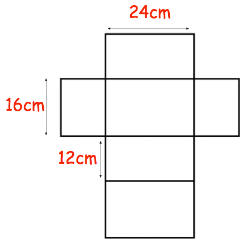
Solution :

From the given net diagram,

Length of cuboid = 24 cm

Width = 16 cm

height = 12 cm

Volume of cuboid = length x width x height

= 24 x 16 x 12

= 4608 cm³

Problem 6 :

Find the surface area of a box with length 12 inches and width and height both 4 inches each.

Solution :

Surface area = 2(l w + w h + h l)

Length = 12 inches, width = height = 4 inches

= 2 (12 x 4 + 4 x 4 + 4 x 12)

= 2 (48 + 16 + 48)

= 2(112)

= 224 inches²

Problem 7 :

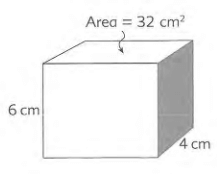
Find the surface area of the shown below.

Solution :

Area of the top = 32 cm²

From the given figure, width = 4 cm and height = 6 cm

length x width = 32

length x 4 = 32

length = 32/4 ==> 8 cm

Surface area of rectangular prism = 2(lw + wh + hl)

= 2 (8 x 4 + 4 x 6 + 6 x 8)

= 2(32 + 24 + 48)

= 2(104)

= 208 cm²

Problem 8 :

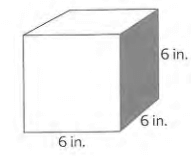
Find the surface area of cube.

Solution :

By observing the measures, it is cube.

Side length of cube = 6 inches

Surface area of cube = 6a²

= 6 (6)²

= 216 cm²

Problem 9 :

The volume of a cuboid is 15,000 𝑐𝑚³. If the length is 30 cm and the width is 25 cm, find the height of the cuboid

Solution :

Volume of cuboid = 15,000 𝑐𝑚³

length = 30 cm, width = 25 cm and height = h

Length x width x height = 15,000 𝑐𝑚³

30 x 25 x h = 15,000

h = (15000) / (30 x 25)

h = 20 cm

Problem 10 :

The ratio of the width of a cuboid to its height is 4:5. Its width is 40 cm. The ratio of the height to the length is 2:3. Find the volume of the cuboid.

Solution :

Width of the cuboid = 4x, height = 5x

Width = 40 cm

4x = 40

x = 10

Width = 4x = 4(10) ==> 40 cm

Height = 5x = 5(10) ==> 50 cm

ratio between height to the length = 2 : 3

2y = height and length = 3y

2y = 50

y = 25

Applying the value of y, we get

Length = 3y = 3(25) ==> 75 cm

Volume of the cuboid = length x width x height

= 75 x 40 x 50

= 150000 cm³

Problem 11 :

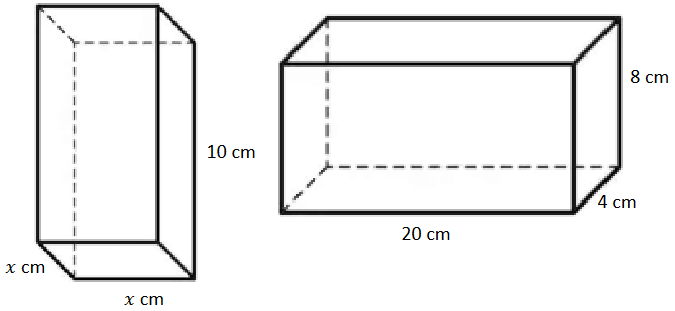
The two cuboids shown below have the same volume. Calculate the value of 𝑥.

Solution :

Volume of cuboid = length x width x height

x(x) (10) = 20 x 4 x 8

10x² = 640

x² = 64

x = 8

So, the value of x is 8 cm.