SOLVING SYSTEM OF INEQUALITIES IN TWO VARIABLES BY GRAPHING
Sketch the solution to each system of inequalities.
Problem 1 :
y ≤ -x-2
y ≥ -5x + 2
Solution :
y ≤ -x - 2 ----(1)
y ≥ -5x + 2
Slope and y-intercept of (1) :
Slope = -1
y-intercept = -2
Since line (1) is having negative slope, it should be a falling line. Rise = -1 and run = 1. Tracing some more points and joining them, we will the line. It should be solid line since we have ≤.
Slope and y-intercept of (2) :
Slope = -5
y-intercept = 2
Since line (2) is having negative slope, it should be a falling line. Rise = -5 and run = 1. Tracing some more points and joining them, we will get the line. It should be solid line since we have ≥.
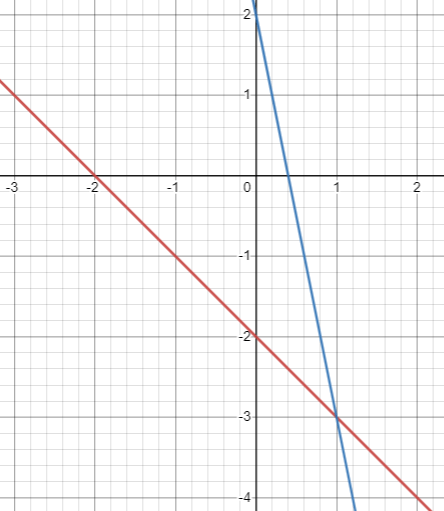
Test point for y ≤ -x - 2 :
|
Below the line (-2, -2) |
y ≤ -x-2 -2 ≤ -(-2)-2 -2 ≤ 2 - 2 -2 ≤ 0 True |
So, the region below y ≤ -x-2 be the solution.
Test point for y ≥ -5x + 2 :
|
Below the line (-2, -2) |
y ≥ -5x + 2 -2 ≥ -5(-2) + 2 -2 ≥ 10 + 2 -2 ≥ 12 False |
So, the region above y ≥ -5x + 2 be the solution. So, overlapping region must be the solution region.
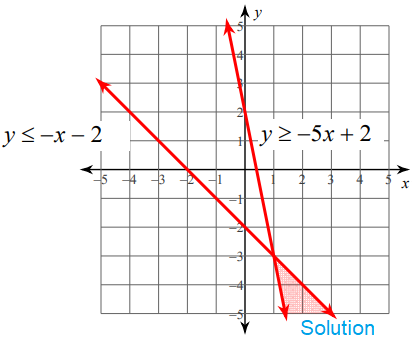
Sketch the solution to each system of Inequalities.
Problem 2 :
y > -x – 2
y < -5x + 2
Solution :
y > -x – 2 --- (1)
y < -5x + 2
Slope and y – intercept of (1) :
Slope = -1
y – intercept = -2
Since line (1) is having negative slope, it should be a falling line. Rise = -1 and run = 1. Tracing some more points and joining them, we will get the line, it should be dotted line since we have >.
Slope and y – intercept of (2) :
Slope = -5
y – intercept = 2
Since line (2) is having negative slope, it should be a falling line. Rise = -5 and run = 1. Tracing some more points and joining them, we will get the line, it should be dotted line since we have <.
Test point for y > -x – 2 :
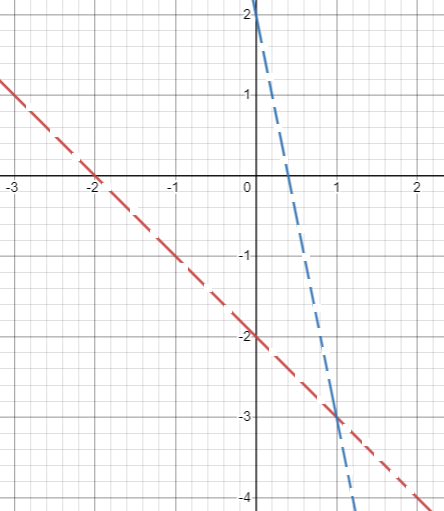
|
Below the line (-2, -2) |
y > -x - 2 -2 > -(-2) – 2 -2 > 2 – 2 -2 > 0 False |
Test point for y < -5x + 2 :
|
Below the line (-2, -2) |
y < -5x + 2 -2 < -5(-2) + 2 -2 < 10 + 2 -2 < 12 True |
So, the region above y
< -5x+2 be the solution. So, overlapping region must be the solution
region.
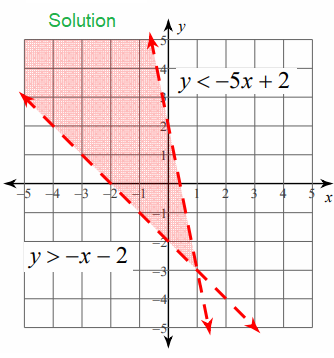
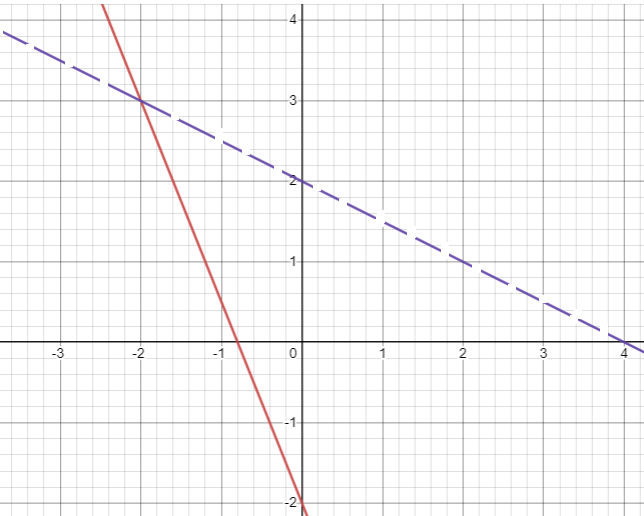
Problem 3 :
y ≤ 1/2x + 2
y < -2x – 3
Solution :
y ≤ 1/2x + 2 --- (1)
y < -2x – 3 --- (2)
Slope and y – intercept of (1) :
Slope = 1/2
y – intercept = 2
Since line (1) is having positive slope, it should be a raising line. Rise = 1 and run = 2. Tracing some more points and joining them, we will get the line, it should be solid line since we have ≤.
Slope and y – intercept of (2) :
Slope = -2
y – intercept = -3
Since line (2) is having negative slope, it should be a falling line. Rise = -2 and run = 1. Tracing some more points and joining them, we will get the line, it should be dotted line since we have <.
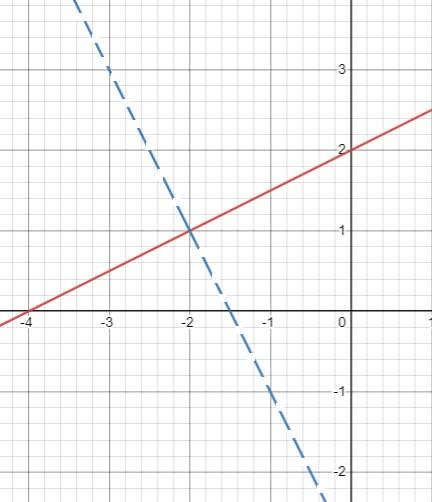
Test point for y ≤ 1/2x + 2 :
Let us take (1, 1) below the line and apply in (1)
1 ≤ (1/2)(1) + 2
1 ≤ 5/2 (True)
Test point for y < -2x – 3 :
Let us take (-2, -2) below the line and apply in (1)
-2 < -2(-2) – 3
-2 < 4 - 3
-2 < 1 (True)
Overlapping region is the solution.
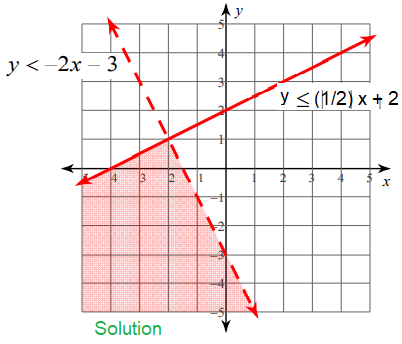
Problem 4 :
x ≤ -3
y < (5/3)x + 2
Solution :
x ≤ -3 --- (1)
y < (5/3)x + 2 --- (2)
Slope and y – intercept of (1) :
It should be the vertical line having x intercept at -3.
Slope and y – intercept of (2) :
Slope = 5/3
y – intercept = 2
Since line (2) is having negative slope, it should be a falling line. Rise = 5 and run = 3. Tracing some more points and joining them, we will get the line, it should be dotted line since we have <.
Test point for y < (5/3)x + 2 :
Let us take (1, 2) below the line and apply in (2)
2 < (5/3)(1) + 2
2 < 11/3 (True)
Overlapping region will be the solution.
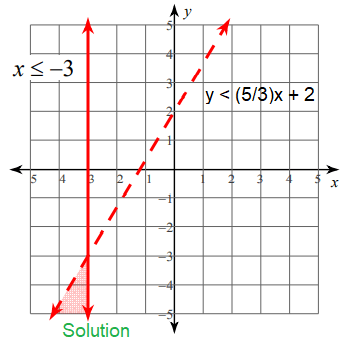
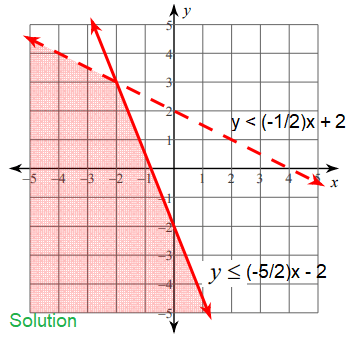
Problem 5 :
y ≤ -(5/2)x - 2
y < -(1/2)x + 2
Solution :
y ≤ -(5/2)x - 2 --- (1)
y < -(1/2)x + 2 --- (2)
Slope and y – intercept of (1) :
Slope = -5/2, y-intercept = -2
Slope and y – intercept of (2) :
Slope = -1/2, y-intercept = 2
Taking a point above the line (-1, 2) and applying in y ≤ -(5/2)x - 2
2 ≤ -(5/2)(-1) - 2
2 ≤ (5/2) - 2
2 ≤ (1/2) (False)
Taking a point below the line (1, 1) and applying in y ≤ -(1/2)x + 2
1 ≤ -(1/2)(1) + 2
1 ≤ (-1/2) + 2
1 ≤ (3/2) (True)
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling