SOLVING REAL LIFE PROBLEMS INVOLVING SLOPE

Problem 1 :

The percent y (in decimal form) of battery power remaining x hours after you turn on a laptop computer is 

y = -0.2x + 1

a)  Graph the equation

b)  Interpret the x and y-intercepts.

c) After how many hours is the battery power at 75%.

Solution :

y = -0.2x + 1

a) From the equation above, we know that y-intercept is 1 and slope is 0.2. We can draw the falling line.

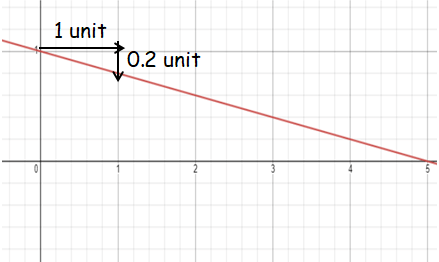
b)  y = -0.2x + 1

The x-intercept is 5. So, the battery lasts 5 hours. The y-intercept is 1. So, the battery power is at 100% when you turn on the laptop

c)  x - number of hours, y - remaining quantity of battery power

Remaining quantity of battery power = 75% ==> 0.75

-0.2x + 1 = 0.75

-0.2x = 0.75 - 1

-0.2x = -0.25

x = 0.25/0.2

x = 1.25

After 1.25 hours, the battery will have power of 75%.

Problem 2 :

The amount y (in gallons) of gasoline remaining in a gas tank after driving x hours is

y = −2x + 12

(a) Graph the equation.

(b) Interpret the x- and y-intercepts.

(c) After how many hours are there 5 gallons left?

Solution :

a)  Slope = -2, y-intercept = 12

Since it has negative slope, it must be a falling line.

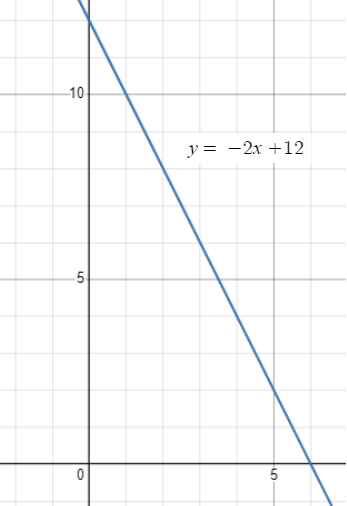
b)  y = −2x + 12

After 6 hours only, the quantity of gasoline will become 0.

Initially capacity of the tank is 12 gallons.

c)  Number of gallons left = 5

-2x + 12 = 5

-2x = 5 - 12

-2x = -7

x = 7/2

x = 3.5

After 3.5 hours  gallons left.

Problem 3 :

The graph relates temperatures y (in degrees Fahrenheit) to temperatures x (in degree Celsius)  

a) Find the slope and y-intercept

b) Write an equation of the line

c) What is the mean temperature of Earth in degrees Fahrenheit)

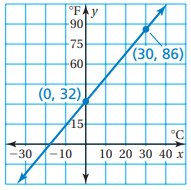
Solution :

Slope :

To find slope, we choose any two points on the straight line.

(0, 32) and (30, 86)

y intercept is at 32.

b)  Slope = 9/5

Equation of the line :

c) Mean temperature :

Problem 4 :

You are downloading a song. The percent y (in decimal form) of megabytes remaining to download after x seconds is

y = −0.1x + 1.

a) Graph the equation.

b) Interpret the x- and y-intercepts.

c) After how many seconds is the download 50% complete?

Solution :

a) Slope = -0.1 and y-intercept is 1

Since we have negative slope, it must be a falling line.

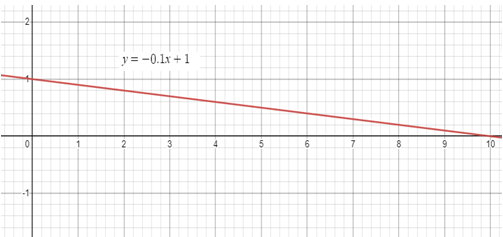
b) Interpret the x- and y-intercepts.

y = −0.1x + 1

c) After how many seconds is the download 50% complete?

y = 50% = 0.50

0.50 = -0.1x + 1

0.50 - 1 = -0.1x

-0.50 = -0.1x

x = 5