SOLVING REAL LIFE PROBLEMS INVOLVING LINEAR FUNCTIONS

Problem 1 :

Felicia Johnson paid $125 to join a tennis club. She pays an additional $5 every time she uses one of the club's tennis courts. Use this information to answer the following questions.

a. Write an equation that describes Felicia's total cost for playing tennis as a function of the number of times she plays. Let C = the total cost and n = the number of times she plays.

b. Describe the domain and range of the function.

c. Felicia does not want to spend more than $275 to play tennis during the summer.

What is the maximum number of times that she can play tennis on the club's courts for this amount?

Solution :

Amount paid by Felicia Johnson initially = $125

a) For every hour of using tennis court, he has to pay $5 and n be the number of times she pays.

Total cost (C) = 125 + 5n

b)  Domain :

Possible values of n are, all whole numbers.

Even he is not using tennis court once, he has to pay $125.

So, range is 125, 130, 135, .........

c)  She doesn't want to spend more than 250.

C ≤ 125 + 5n

275 ≤ 125 + 5n

Subtracting 125 on both sides, we get

150 ≤ 5n

Dividing by 5, we get

30 ≤ n

So, he can use the tennis court maximum at 30 times.

Problem 2 :

Members of the soccer team are walking to raise money for a local shelter. 92 sponsors pledged a dollar per kilometer. Some sponsors gave additional donations that did not depend on the distance students walked.

a. Write a verbal model that relates the total amount A of money raised by the soccer team to the number n of kilometers walked and the amount d given in additional donations.

b. The team walked 8 kilometers and raised a total amount of $842. Is there enough information to find how much money came from additional donations that did not depend on walking distance? If so, find this amount.

Solution :

Total amount raised, A, equals 92 sponsors times number of kilometers, n, times $1 per kilometer, plus additional donations, d.

So, A = 92n + d

b)  To find the additional donation, we have enough information.

A = 842 and n = 8

842 = 92 (8) +d 

d = 842 - 736

d = 106

Problem 3 :

A grocer knows that if he sells his canned hams for $8 each, he can sell 950 per month, and if he sells the same hams for $10, he will sell 900 per month. Assuming the relationship between price and sales is linear, write an equation you could use to predict sales for other prices.

Solution :

Let x be the price and y be the sales per month.

Creating linear relationship between x and y, we create the equation in the form

y = mx + b ----(1)

(8, 950) and (10, 900)

m = (900 - 950) / (10 - 8)

m = -50/2

m = -25

Applying the value of m in (1), we get

y = -25x + b

Applying one of the point (8, 950) in the equation above to get the value of b, we get

950 = -25(8) + b

950 = -200 + b

b = 950 + 200

b = 1150

y = -25x + 1150

Problem 4 :

If a large factory sells its new gadgets for $5 each, it can sell 1050 per month, and if it sells the same gadgets for $9, it will sell 900 per month. Assuming the relationship between price and sales is linear, predict the monthly sales of gadgets to the nearest whole number if the price is $12.

Solution :

Let x be the price of each gadgets and y be the sales per month.

Linear relationship between the variables x and y :

y = mx + b ----(1)

(5, 1050) and (9, 900)

Slope (m) = (900 - 1050) / (9 - 5)

m = -150 / 4

m = -37.5

y = -37.5 x + b

Applying the point (5, 1050) in (1), we get

1050 = -37.5 (5) + b

1050 = -187.5 + b

b = 1050 + 187.5

b = 1237.5

y = -37.5 x + 1237.5

Monthly sales, when price = 12

y = -37.5(12) + 1237.5

y = -450 + 1237.5

y = 787.5

So, the sales for the month is $788 when price is $12.

Problem 5 :

A balloon is released from the top of a building. The graph shows the height of the balloon over time

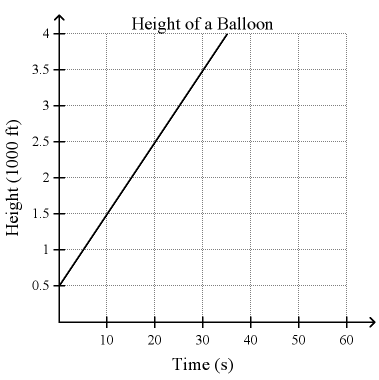
a. What does the slope and y-intercept reveal about the situation?

b. For a similar situation, the slope 35 is and the y-intercept is 550. What can you conclude?

Solution :

a)  Rise = 2.5 - 1.5 ==> 1 ==> 1000 ft

Run = 20 - 10 ==> 10 seconds

For every 10 seconds, it increases the height of 1000 ft.

b)  The balloon starts at a height of 500, and rises at a rate of 100; The balloon starts at a heigh of 550, and rises at a rate of 35.