SOLVING RATIONAL INEQUALITIES

How to solve rational inequalities ?

The standard forms of rational inequalities are below :

(ax + b) / (cx + d) > 0
(ax + b) / (cx + d) < 0
(ax + b) / (cx + d) ≥ 0
((ax + b) / (cx + d) ≤ 0

Step 1 :

Make sign of coefficient of x as positive, if they are not.

Step 2 :

Equate the numerator and denominator to zero and find the values of x. These values are known as critical numbers.

Step 3 :

By applying the x values on a number line, we find the intervals.

Step 4 :

We will choose random values from intervals and apply the given function.

If f(x) is being satisfied by the values we choose from the interval, then that interval or intervals are known as the solution.

Solve each inequality.

Problem 1 :

(x - 7)/(x - 1) < 0

Solution :

Let f(x) = (x - 7)/(x - 1)

f(x) < 0

(x - 7)/(x - 1) < 0

By equating the numerator and denominator to zero, we get

x - 7 = 0, x - 1 = 0

x = 7 and x = 1 (critical numbers)

The critical numbers are dividing the number line into three intervals.

Intervals	Choosing value f(x) from intervals	f(x)
(-∞, 1)	0 Є (-∞, 1)	f(x) > 0
(1, 7)	2 Є (1, 7)	f(x) < 0
(7, ∞)	8 Є (7, ∞)	f(x) > 0

From the above, the possible values of x are

1 < x < 7

By writing it as interval notation, we get

(1, 7)

So, the required solution is 1 < x < 7

Problem 2 :

(x + 5)/(x - 4) ≤ 0

Solution :

Let f(x) = (x + 5)/(x - 4)

f(x) ≤ 0

(x + 5)/(x - 4) ≤ 0

By equating the numerator and denominator to zero, we get

x + 5 = 0, x - 4 = 0

x = -5 and x = 4 (critical numbers)

The critical numbers are dividing the number line into three intervals.

Intervals	Choosing value f(x) from intervals	f(x)
(-∞, -5]	-6 Є (-∞, -5)	f(x) ≥ 0
[-5, 4)	0 Є [-5, 4)	f(x) ≤ 0
(4, ∞)	5 Є (4, ∞)	f(x) ≥ 0

From the above, the possible values of x are

-5 ≤ x < 4

By writing it as interval notation, we get

[-5, 4)

So, the required solution is -5 ≤ x < 4.

Problem 3 :

(x + 32)/(x + 6) ≤ 3

Solution :

Let f(x) = (x + 32)/(x + 6)

f(x) ≤ 3

(x + 32)/(x + 6) ≤ 3

Subtract 3 on both sides, we get

(x + 32)/(x + 6) - 3 ≤ 3 - 3

Taking least common multiple, we get

[(x + 32)/ -3(x + 6)]/ (x + 6) ≤ 0

(x + 32 - 3x - 18)/(x + 6) ≤ 0

(-2x + 14)/(x + 6) ≤ 0

By equating the numerator and denominator to zero, we get

-2x + 14 = 0 and x + 6 = 0

-2x = -14 and x = -6

x = 7 and x = -6

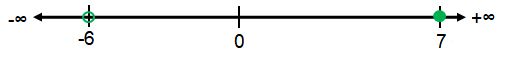
Intervals	Choosing value f(x) from intervals	f(x)
(-∞, -6)	-7 Є (-∞, -6)	f(x) ≤ 0
(-6, 7]	0 Є (-6, 7]	f(x) ≥ 0
[7, ∞)	8 Є [7, ∞)	f(x) ≤ 0

From the table, the possible values of x are

x < -6 or x ≥ 7

By writing it as interval notation, we get

(-∞, -6) υ [7, ∞)

So, the required solution is x ≤ -6 or x > 7

Problem 4 :

(x + 68)/(x + 8) ≥ 5

Solution :

Let f(x) = (x + 68)/(x + 8)

f(x) ≥ 5

(x + 68)/(x + 8) ≥ 5

Subtract 5 on both sides, we get

(x + 68)/(x + 8) - 5 ≥ 5 - 5

Taking least common multiple, we get

(x + 68) -5(x + 8)/(x + 8) ≥ 0

(x + 68 - 5x - 40)/(x + 8) ≥ 0

(-4x + 28)/(x + 8) ≥ 0

By equating the numerator and denominator to zero, we get

-4x + 28 = 0 and x + 8 = 0

-4x = -28 and x = -8

x = 7 and x = -8

Intervals	Choosing value f(x) from intervals	f(x)
(-∞, -8)	-9 Є (-∞, -8)	f(x) ≤ 0
(-8, 7]	0 Є (-8, 7]	f(x) ≥ 0
[7, ∞)	8 Є [7, ∞)	f(x) ≤ 0

From the above, the possible values of x are

-8 < x ≤ 7

By writing it as interval notation, we get

(-8, 7]

So, the required solution is -8 < x ≤ 7.

Problem 5 :

(x + 3) (x + 5) / (x + 2) ≥ 0

Solution :

Let f(x) = (x + 3) (x + 5) / (x + 2)

f(x) ≥ 0

(x + 3) (x + 5) / (x + 2) ≥ 0

By equating the numerator and denominator to zero, we get

x + 3 = 0, x + 5 = 0, and x + 2 = 0

x = -3, x = -5, and x = -2

Intervals	Choosing value f(x) from intervals	f(x)
(-∞, -5]	-6 Є (-∞, -5]	f(x) ≤ 0
[-5, -3]	-4 Є [-5, -3]	f(x) ≥ 0
[-3, -2)	-3 Є [-3, -2)	f(x) ≤ 0
(-2, ∞)	0 Є [-2, ∞)	f(x) ≥ 0

From the table, the possible values of x are

-5 ≤ x ≤ -3 or x > -2

By writing it as interval notation, we get

[-5, -3] υ (-2, ∞)

So, the required solution is -5 ≤ x ≤ -3 or x > -2.

SOLVING RATIONAL INEQUALITIES

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling