SOLVING PROBLEMS WITH LINES AND ANGLES

In geometry, parallel lines can be defined as two lines in the same plane that are at equal distance from each other and never meet. They can be both horizontal and vertical.

We can see parallel lines examples in our daily life like a zebra crossing, the lines of notebooks, and on railway tracks around us. 

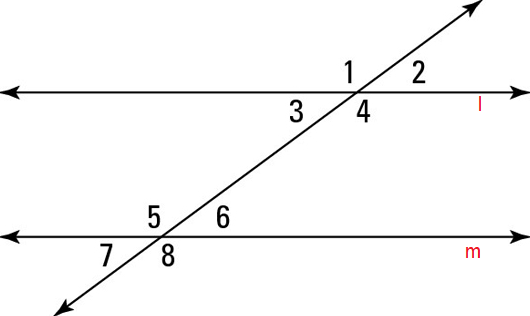
Here l and m are parallel lines and we see 8 angles are created.

Corresponding angles :

∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8

Vertically opposite angles :

∠1 = ∠4, ∠3 = ∠2, ∠5 = ∠8, ∠7 = ∠6

Alternate interior angles :

∠3 = ∠6, ∠4 = ∠5

Co interior angles are supplementary :

∠3 + ∠5 = 180

∠4 + ∠6 = 180

Problem 1 :

If the complement of an angle is equal to the supplement of four times the angle, then find the measure of the angle.

Solution :

Let x be the angle.

Complement of an angle is 90^º - x.

Supplementary angle is 180^º - x.

To find the measure of the angle :

90^º - x = 180^º – 4x

-x + 4x = 180^º – 90^º

3x = 90^º

Dividing 3 on each sides.

3x/3 = 90^º/3

x = 30^º

So, the measure of the angle is 30^º.

Problem 2 :

In a triangle ∠ABC, ∠A + ∠B = 110^º, ∠C + ∠A = 135^º, Find ∠A.

Solution :

Sum of interior angles of a triangle = 180^º

∠A + ∠B + ∠C = 180^º

110^º + ∠C = 180^º

∠C = 180^º - 110^º

∠C = 70^º

∠B + ∠C + ∠A = 180^º

135^º + ∠B = 180^º

∠B = 180^º - 135^º

∠B = 45^º

∠A + ∠B + ∠C = 180^º

∠A + 45^º + 70º = 180^º

∠A + 115^º = 180^º

∠A = 180^º - 115^º

∠A = 65^º

Problem 3 :

In the given figure, what value of x will make AOB a line ?

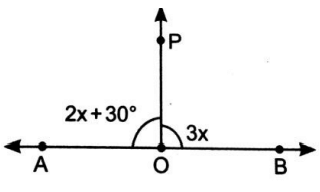
Solution :

∠AOP + ∠BOP = 180^º

2x + 30 + 3x =  180^º

5x + 30 =  180^º

5x = 180 - 30

5x = 150

x = 150/5

x = 30

Problem 4 :

In the given figure, AB//ED, find x.

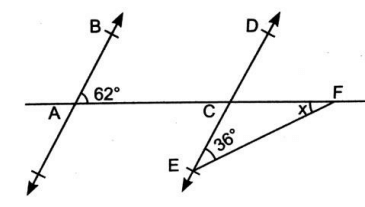
Solution :

AB and ED is a parallel line.

∠BAC = ∠DCF = 62^º (corresponding angles)

∠ECF + ∠DCF = 180^º

∠ECF + 62^º = 180^º

∠ECF = 180^º - 62^º

∠ECF = 118^º

∠ECF is a triangle.

∠ECF + ∠CEF + ∠EFC = 180^º

118^º + 36^º + x^º = 180^º

154^º + x^º = 180^º

x^º = 180^º - 154^º

x^º = 26^º

Problem 5 :

Determine the value of x in the given figure if AB||CD||EF

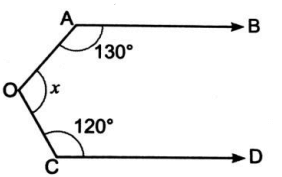
Solution :

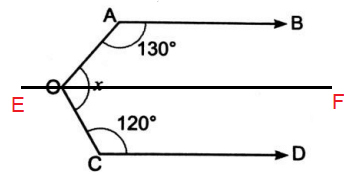
∠AOF + ∠OAB = 180 (Cointerior angles) ---(1)

∠DCO + ∠COF = 180 (Cointerior angles) ---(2)

From (1)

∠AOF + 130 = 180

Subtracting 130

∠AOF = 50

From (2)

120 + ∠COF = 180

Subtracting 120, we get

∠COF = 60

x = ∠AOF + ∠COF

x = 50 + 60

x = 110

Problem 6 :

Determine the value of x in the given figure if AB||CD||EF

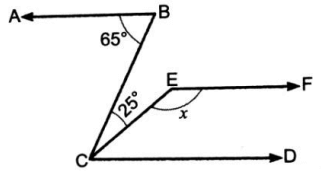
Solution :

Since EF and CD are parallel,

∠DCE + ∠CEF = 180

∠DCE + x = 180

∠DCE = 180 - x

Since AB and CD are parallel.

∠ABC = ∠BCD (alternate interior angles)

65 = 25 + 180 - x

x = 25 + 180 - 65

x = 140

Problem 7 :

In a triangle if 4∠A = 3∠B = 12∠C, find all the angles.

Solution :

 4∠A = 3∠B = 12∠C = x

Sum of interior angle is 180^º.

∠A + ∠B + ∠C = 180^º

x/4 + x/3 + x/12 = 180

(x/4 × 3/3) + (x/3 × 4/4) + x/12 = 180

(3x + 4x + x)/12 = 180

8x/12 = 180

8x = 180 × 12

8x = 2160

Dividing 8 on both sides.

x = 2160/8

x = 270

Substitute the value x = 270 in equation (1), (2) and (3).

So, the angles are ∠A = 67.5^º, ∠B = 90^º and ∠C = 22.5^º.

Problem 8 :

The angles of a triangle are in the ratio 3 : 7 : 8. Find the angles of the triangle.

Solution :

Let the angles of a triangle are in the ratio be 3x, 7x, and 8x.

3x + 7x + 8x = 180^º

18x = 180^º

Dividing 18 on each sides.

x = 180^º/18

x = 10^º

To find the angles of the triangle :

3 × 10^º = 30^º

7 × 10^º = 70^º

8 × 10^º = 80^º

So, the angles of the triangle is 30^º, 70^º and 80^º.

Problem 9 :

In the given figure find the value of x.

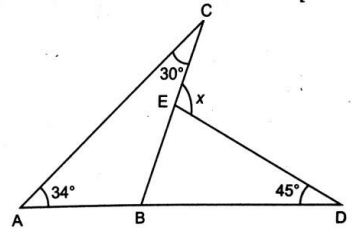
Solution :

In a triangle ∠ABC,

∠ABC = 180 - (∠CAB + ∠ACB)

∠ABC = 180^º - (34^º + 30^º)

∠ABC = 116^º

∠ABC + ∠CBD = 180

116 + ∠CBD = 180

∠CBD = 64

In a triangle ∠EBD,

∠EBD + ∠BDE + ∠DEB = 180^º

64^º + 45^º + ∠DEB = 180^º

109^º + ∠DEB = 180^º

∠DEB = 180^º - 109^º

∠DEB = 71^º

∠DEB + x = 180^º

71^º + x = 180^º

x = 180^º - 71^º

x = 109^º