SOLVING NONLINEAR SYSTEMS OF EQUATIONS

Solve the nonlinear system. Justify your answer with a graph.

Problem 1 :

y² = x − 3 and y = x - 3

Solution :

y² = x − 3 -------(1)

and

y = x - 3 -------(2)

Apply (2) in (1)

(x - 3)² = x - 3

x² - 2x(3) + 3² = x - 3

x² - 6x + 9 = x - 3

x² - 6x -x + 9 + 3 = 0

x² - 7x+ 12 = 0

(x - 4) (x - 3) = 0

Equating each factor to 0, we get

x = 4 and x = 3

So, the point of intersections are (4, 1) and (3, 0).

Check with graph :

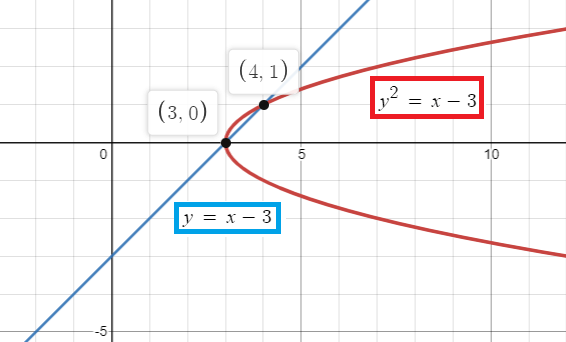
Problem 2 :

y² = 4x + 17 and y = x + 5

Solution :

y² = 4x + 17 -----(1)

and

y = x + 5 -----(2)

Applying (2) in (1), we get

(x + 5)² = 4x + 17

x² + 2x(5) + 5² = 4x + 17

x² + 10x +25 = 4x + 17

x² + 10x - 4x +25 - 17 = 0

x² + 6x + 8 = 0

(x + 2)(x + 4) = 0

Equating each factor to zero, we get

x = -2 and x = -4

So, the point of intersections are (-2, 3) and (-4, 1)

Check with graph :

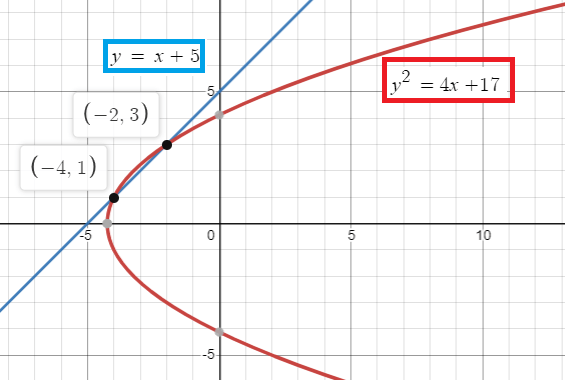
Problem 3 :

x² + y² = 4

y = x - 2

Solution :

x² + y² = 4 -------(1)

y = x - 2 -------(2)

Applying (2) in (1), we get

x² + (x - 2)² = 4

x² + x² - 2x(2) + 2² = 4

2x² - 4x + 4 = 4

Subtracting 4 on both sides, we get

2x² - 4x  = 0

2x(x - 2) = 0

2x = 0 and x - 2 = 0

x = 0 and x = 2

When x = 0, then y = 0 - 2 ==> -2

When x = 2, then y = 2 - 2 ==> 0

So, the points of intersections are (0, -2) and (2, 0).

Problem 4 :

x² + y² = 25

y = (-3/4)x + (25/4)

Solution :

x² + y² = 25 ----(1)

y = (-3/4)x + (25/4) -----(2)

Applying (2) in (1), we get

(x - 3) (x - 3) = 0

x = 3 and x = 3

When x = 3, then y = (-3/4)(3) + (25/4)

y = -9/4 + 25/4

y= 16/4

y = 4

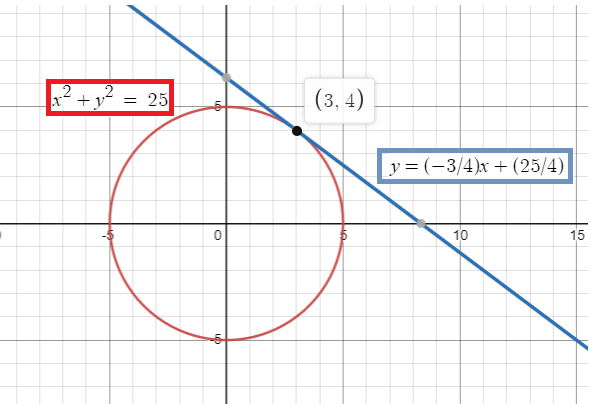
Problem 5 :

Use the graphs of the linear and quadratic functions.

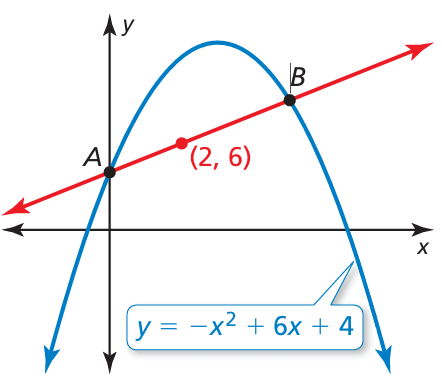
a. Find the coordinates of point A.

b. Find the coordinates of point B.

Solution :

a)  By observing thea graph given above, Point A will be (0, y)

y = -x² + 6x + 4

y = -0² + 6(0) + 4

y = 4

So, the required point A will be (0, 4).

b) Two point on the line are (0, 4) and (2, 6)

Slope = (6 - 4) / (2 - 0)

= 2/2

= 1

Equation of the line :

y - y₁ = m(x - x₁)

(y - 4) = 1(x - 0)

y = x + 4

Solving the system of equations, we get

y = x + 4 ------(1)

y = -x² + 6x + 4 ------(2)

(1) = (2)

x + 4 = -x² + 6x + 4

x² + x - 6x = 0

x² - 5x = 0

x(x - 5) = 0

x = 0 and x = 5

Applying the value of x, we get

So, the required points are (0, 4) and (5, 9). Point B is (5, 9).