SOLVING LOGARITHMIC INEQUALITIES

To solve logarithmic inequalities, we have to follow the procedure given below.

Step 1 :

Replace the inequality sign as equal sign.

Step 2 :

Using the properties of logarithm, we have to simplify and solve for the variable.

Note :

When log _y x > k, if y > 1, then x > y^k
When log _y x > k, if 0 < y < 1, then x < y^k

The problem can be solved using change base rule, the detailed example is given below.

Step 3 :

Find the domain for each logarithmic expressions and plot in the number line.

Step 4 :

The intersection of all domain is the value of x in the given logarithmic expression.

Solve the following logarithmic inequalities.

Problem 1 :

Solution :

5x - 1 ⩾ 0

5x ⩾ 1

x ⩾ 1/5

Domain of the given logarithmic expression is [1/5, ∞)

Alternate way :

Domain of (-∞, 2/5)

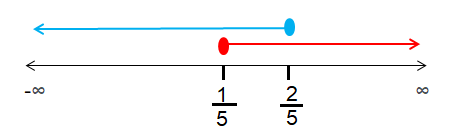
The intersection of the domain is (1/5, 2/5).

Problem 2 :

Solution :

Domain of logarithmic expression :

3x - 1 > 0

3x > 1

x > 1/3

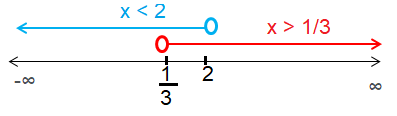
The solution is (1/3, 2).

Problem 3 :

Solution :

Domain of logarithmic expression :

6/x > 0

x > 0

x + 5 > 0

x > -5

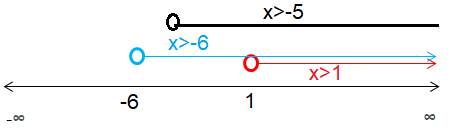
All negative values are ignored and the intersection part is (0, 1).

Problem 4 :

Solution :

Domain of logarithmic expressions :

2x - 6 > 0

2x > 6

x > 3

2x - 1 > 0

2x > 1

x > 1/2

All negative values should be ignored for x and finding the intersection part, we get (1/2, ∞).

Problem 5 :

Solution :

Domain of logarithmic expressions :

3 - 2x > 0

-2x > -3

x < 3/2

4x + 1 > 0

4x > -1

x > -1/4

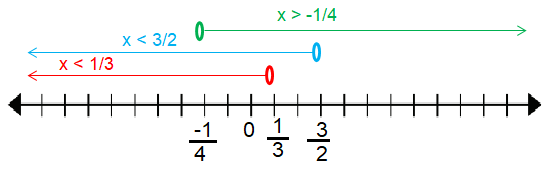
The intersection part of all is (-1/4, 1/3).

Problem 6 :

Solution :

Domain of logarithmic expressions :

10x + 3 > 0

10x > -3

x > -3/10

7x - 4 > 0

7x > 4

x > 4/7

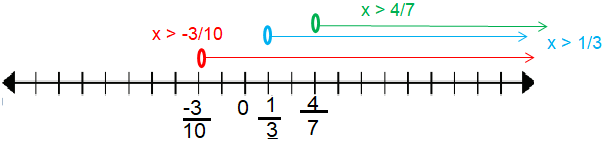
Intersection of all domains is (4/7, ∞).

Problem 7 :

Solution :

Negative values are not solution. Only positive values greater than 1. So, the solution is (1, ∞).

SOLVING LOGARITHMIC INEQUALITIES

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling