SOLVING LOARITHMIC EQUATIONS WITH BASE

To solve logarithmic equation, first we should know how to convert the logarithmic form to exponential form.

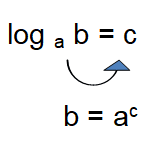
Step 1 :

Move the base to the other side of the equal sign.

Step 2 :

Create the same base on both sides.

Step 3 :

Using the properties of exponents, if the bases are same on both sides of the equal sign, then we can equate the powers.

Find the value of y.

Problem 1 :

log₅ 25 = y

Solution :

In logarithmic form :

log₅ 25 = y

Converting into exponential form :

5^y = 25

Write 25 as base of 5.

5^{y =} 5²

Since bases are equal, we equate the powers.

y = 2

Problem 2 :

log₃1 = y

Solution :

In logarithmic form :

log₃ 1 = y

Converting into exponential form :

3^y = 1

3^y = 3⁰ (3⁰ = 1)

Since bases are equal, we equate the powers.

y = 0

Problem 3 :

log₁₆ 4 = y

Solution :

In logarithmic form :

log₁₆ 4 = y

Converting into exponential form :

16^y = 4

(2⁴)^y = 2²

2^4y = 2²

4y = 2

y = 2/4

y = 1/2

Problem 4 :

log₂ (1/8) = y

Solution :

In logarithmic form :

log₂ (1/8) = y

Converting into exponential form :

2^y = 1/8

 2^y = 2^-3 (2^-3 = 1/8)

y = -3

Problem 5 :

log₅1 = y

Solution :

In logarithmic form :

log₅ 1 = y

Converting into exponential form :

5^y = 1

5^y = 5⁰ (5⁰ = 1)

y = 0

Problem 6 :

log₂ 8 = y

Solution :

In logarithmic form :

log₂ 8 = y

Converting into exponential form :

2^y = 8

2^{y =} 2³ (2³ = 8)

y = 3

Problem 7 :

log₇ (1/7) = y

Solution :

log₇ (1/7) = y

Converting from logarithmic form to exponential form, we get

7^y = 1/7

 7^y = 7 ^-1 (7^-1 = 1/7)

y = -1

Problem 8 :

log₃ (1/9) = y

Solution :

log₃ (1/9) = y

Converting from logarithmic form to exponential form, we get

3^y = 1/9

 3^y = 3^-2 (3^-2 = 1/9)

y = -2

Problem 9 :

log_y 32 = 5

Solution :

log_y 32 = 5

Converting from logarithmic form to exponential form, we get

y⁵ = 32

y⁵ = 2⁵

Since powers are equal, we equate the bases.

So,

y = 2

Problem 10 :

log₉ y = -1/2

Solution :

log₉ y = -1/2

9^-1/2 = y

(3²)^-1/2 = y

3^-1 = y

y = 1/3

Problem 11 :

log₄ (1/8) = y

Solution :

y = log_b x ó b^y = x

log₄ (1/8) = y

4^y = 1/8

(2²)^y = 1/2³

2^2y = 2^-3

2y = -3

y = -3/2

Problem 12 :

Log₉ (1/81) = y

Solution :

log₉ (1/81) = y

9^y = 1/81

 9^y = 9^-2

Since bases are equal, we equate the powers.

So,

y = -2