SOLVING LINEAR INEQUALITIES IN ONE VARIABLE REVIEW

Problem 1 :

What are the solutions to the following inequality ?

4x ≥ 68

A. x > 64 B. x ≥ 64 C. x > 17 D. x ≥ 17

Solution :

4x ≥ 68

Dividing 4 on both sides.

4/4x ≥ 68/4

x ≥ 17

So, the solutions is x ≥ 17.

Hence, option D. is correct.

Problem 2 :

What are the solutions to the following inequality ?

2x + 6 < 4

A. x < 1 B. x < -1 C. x > 1 D. x > -1

Solution :

2x + 6 < 4

Subtracting 6 on both sides.

2x + 6 – 6 < 4 – 6

2x < -2

Dividing 2 on both sides.

2x/2 < -2/2

x < -1

So, the solutions is x < -1.

Hence, option B. is correct.

Problem 3 :

Melissa has $20 to buy bagels and juice for her class.

Box of bagels  $6.13, including tax

Bottle of juice $2.08, including tax

She will buy one box of bagels, with the rest of the money, Melissa will buy as many bottles of juice as possible. Which inequality can she use to find b, the maximum number of bottles of juice she can buy ?

A. 6.13b + 2.08 ≤ 20.00    B. 6.13 + 2.08b ≤ 20.00 

C.6.13b + 2.08 ≥ 20.00     D. 6.13 + 2.08b ≥ 20.00

Solution :

She will buy one bag of bagels. So, we have to use 6.13. The rest of the money spent for juice. Since b will represents number of bottles of juice.

6.13 + 2.08b ≤ 20.00

Hence, option B. is correct.

Problem 4 :

The picture of the balance shown below models an inequality.

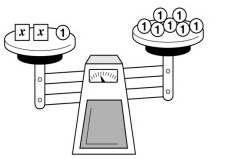
What solutions make the inequality true ?

A.x > 3  B x < 3  C x > 6  D x < 6

Solution :

By observing the graph,

2x + 1 > 7

Subtracting 1 on both sides.

2x + 1 – 1 > 7 – 1

2x > 6

Dividing 2 on both sides.

2x/2 > 6/2

x > 3

Hence, option B. is correct.

Problem 5 :

Which inequality best represents the solution set shown on the number line?

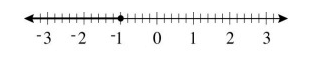
A. n < -1 B. n ≤ -1 C. n > -1 D. n ≥ -1

Solution :

The shaded region has values which are lesser than -1. Since we have closed circle, we will use less than or equal sign.

n ≤ -1

Hence, option B. is correct.

Problem 6 :

Which graph best represents the solution set for the following inequality ?

5n + 2 ≤ 12

Solution :

5n + 2 ≤ 12

Subtracting 2 on both sides.

5n + 2 – 2 ≤ 12 – 2

5n ≤ 10

Dividing 5 on both sides.

5n/5 ≤ 10/5

n ≤ 2

Hence, option B. is correct.

Problem 7 :

When x is an integer, what is the solution set of 5 ≤ x < 8 ?

A. [5, 6, 7, 8]      B. [5, 6, 7] 

C. [6, 7, 8]     D [6, 7]

Solution :

x is an integer

5 ≤ x < 8

After 5, we have less than or equal sign. So, we can include 5 also.

Possible values of x are {5, 6, 7}. 8 is not included because we have just less than before 8.

Hence, option B. is correct.

Problem 8 :

The inequality 3x + 2 > x + 8 is equivalent to

A. x > -1/2  B. x  > 3/2 C. x > 3 D. x < 3

Solution :

3x + 2 > x + 8

Subtracting 2 on both sides.

3x + 2 - 2 > x + 8 – 2

3x > x + 6

Subtracting x on both sides.

3x – x > x + 6 – x

2x > 6

Dividing 2 on both sides.

2x/2 > 6/2

x > 3

Hence, option C. is correct.

Problem 9 :

Chris runs a barber’s shop. It costs him 20 per day to cover his expenses and he charges 4 for every hair cut

(a) Explain why his profit for any day is (4x – 20), where x is the number of haircuts in that day.

He hopes to make at least 50 profit per day, but does not intend to make more than 120 profit.

(b) Write down an inequality to describes this situation.

(c) Solve the inequality.

Solution :

Charge for each hair cut = 4

Let x be the number of hair cuts.

His expenses every day = 20

The earnings other than his expenses can be considered as profit.

So, profit = 4x - 20

b)  His profit should be greater than 50 and lesser than 120.

50 ≤ 4x - 20 ≤ 120

c)  50 + 20 ≤ 4x - 20 + 20 ≤ 120 + 20

70 ≤ 4x ≤ 140

Divide by 4, we get

70/4 ≤ x ≤ 140/4

17.5 ≤ x ≤ 35

Problem 10 :

The distance that a car can travel on a full tank of petrol varies between 200 and 320 miles.

(a) If m represents the distance (in miles) travelled on a full tank of petrol, write down an inequality involving m

(b) Distance in kilometers, k, are related to distances in miles by

m = 5k/8.

Write down an alternative inequality involving k instead of m.

(c) How many kilometers can the car travel on a full tank of petrol ? 

Solution :

The distance between 200 and 320 miles.

(a) If m represents the distance

So, the inequality is 200 ≤ m ≤ 320

(b) Distance in kilometers, 

m = 5k/8

8m = 5k

k = 8m/5

c)  200 ≤ m ≤ 320

200 ≤ 5k/8 ≤ 320

Solving for k, we get

Multiplying by 8,

200(8) ≤ 5k ≤ 320(8)

Dividing by 5, we get

200(8)/5 ≤ k ≤ 320(8)/5

320 ≤ k ≤ 512

So, they can travel between 320 km to 512 km.