SOLVING INEQUALITIES BY MULTIPLYING OR DIVIDING
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Using inverse operations, we solve the inequality given.
To remove the numerical value which is multiplied, we have to divide it on both sides.
To remove the numerical value which is divided, we have to multiply it on both sides.
Properties of Inequalities of Multiplication or Division :
When we multiply or divide the inequality by negative values, we have to flip the inequality sign.
Use a table to solve the inequality.
Problem 1 :
4x < 4
Solution :
4x < 4
Divide it by 4 both sides.
4x/4 < 4/4
x < 1
Problem 2 :
-2x ≤ 2
Solution :
-2x ≤ 2
Divide by -2 on both sides.
x ≥ 2/(-2)
x ≥ -1
Problem 3 :
-5x > 15
Solution :
-5x > 15
Divide it by -5 on both sides.
x < 15/(-5)
x < -3
Problem 4 :
x/-3 ≥ 1
Solution :
x/-3 ≥ 1
Divide it by -3 on both sides.
x ≤ 1/(-3)
x ≤ -3
Problem 5 :
x/-2 > 5/2
Solution :
x/-2 > 5/2
Multiply by -2 on both sides.
x < -5
Problem 6 :
x/4 ≤ 3/8
Solution :
x/4 ≤ 3/8
Multiply by 4 on both sides, we get
x ≤ (3/8)⋅4
x ≤ (3/2)
Solve the inequality. Graph the solution.
Problem 1 :
3n > 18
Solution :
3n > 18
Divide each side by 3.
3n/3 > 18/3
n > 6
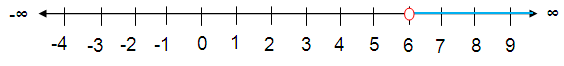
Problem 2 :
c/4 ≤ -9
Solution :
c/4 ≤ -9
Multiply each side by 4.
(c/4) × 4 ≤ -9 × 4
c ≤ -36
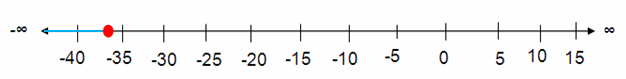
Problem 3 :
1.2m < 12
Solution :
1.2m < 12
Divide each side by 1.2.
(1.2/1.2)m < 12/1.2
m < 10

Problem 4 :
-14 > x ÷ 2
Solution :
-14 > x ÷ 2
Multiply each side by 2.
-14 × 2 > (x/2) × 2
-28 > x
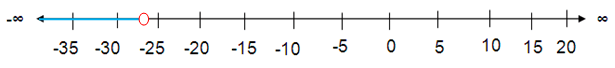
Problem 5 :
w/5 ≥ -2.6
Solution :
w/5 ≥ -2.6
Multiply each side by 5.
(w/5) × 5 ≥ -2.6 × 5
w ≥ -13

Problem 6 :
5 < 2.5k
Solution :
Given, 5 < 2.5k
Divide each side by 2.5.
5/2.5 < 2.5/2.5k
2 < k
k > 2
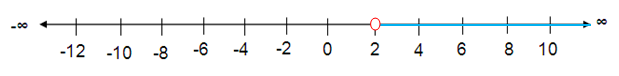
Problem 7 :
4x ≤ -3/2
Solution :
Given, 4x ≤ -3/2
Multiply each side by 2.
(4x) × 2 ≤ (-3/2) × 2
8x ≤ -3
Divide each side by 8.
(8x)/8 ≤ -3/8
x ≤ -3/8

Problem 8 :
2.6y ≤ -10.4
Solution :
Given, 2.6y ≤ -10.4
Divide each side by 2.6.
2.6/2.6y ≤ -10.4/2.6
y ≤ -4
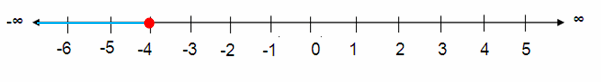
Problem 9 :
10.2 > b/3.4
Solution :
Given,10.2 > b/3.4
Multiply each side by 3.4.
10.2 × 3.4 > (b/3.4) × 3.4
34.68 > b
b < 34.68
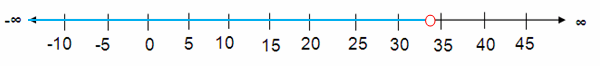
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling