SOLVING FOR MISSING ANGLES IN RIGHT TRIANGLES WITH TRIGONOMETRY

To find missing angles of right triangle, we have to mark which is is hypotenuse, opposite and adjacent.  

Based on the side what we know and the side what we find, including these two information we have to decide which trigonometric ratio should be used.

Find, to one decimal place, the measure of the angle marked θ in :

Problem 1 :

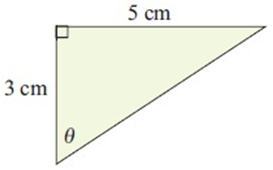
Solution :

Opposite side = 5 cm

Adjacent side = 3 cm

tan θ = opposite/adjacent

tan θ = 5/3

θ = tan^-1 (5/3)

θ = 59.03°

Problem 2 :

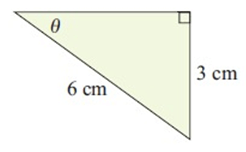
Solution :

Opposite side = 3 cm

Hypotenuse = 6 cm

sin θ = opposite/hypotenuse

sin θ = 3/6

sin θ = 1/2

θ = sin^-1 (1/2)

θ = 30°

Problem 3 :

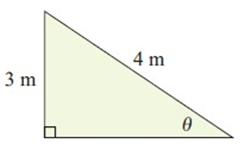
Solution :

Opposite side = 3 m

Hypotenuse = 4 m

sin θ = opposite/hypotenuse

sin θ = 3/4

θ = sin^-1 (3/4)

θ = 48.59°

Problem 4:

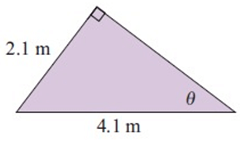
Solution :

opposite side = 2.1 m

Hypotenuse = 4.1 m

sin θ = opposite/hypotenuse

sin θ = 2.1/4.1

θ = sin^-1 (2.1/4.1)

θ = 30.81°

Problem 5 :

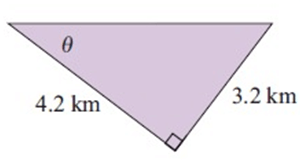
Solution :

Opposite side = 3.2 km

Adjacent side = 4.2 km

tan θ = opposite/adjacent

tan θ = 3.2/4.2

θ = tan^-1 (1.6/2.1)

θ = 37.30°

Problem 6 :

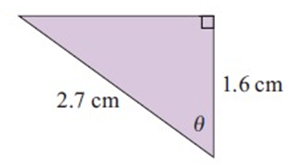
Solution :

Adjacent side = 1.6 cm

Hypotenuse = 2.7 cm

cos θ = adjacent/hypotenuse

cos θ = 1.6/2.7

θ = cos^-1 (1.6/2.7)

θ = 53.65