SOLVING EQUATIONS WITH UNKNOWN IN DENOMINATORS

Problem 1 :

(3x – 8)/2x = 1

Solution :

(3x – 8)/2x = 1

By doing on cross multiplication.

3x – 8 = 2x

3x – 2x = 8

x = 8

Problem 2 :

5x/(2x – 1) = 2

Solution :

5x/(2x – 1) = 2

By doing on cross multiplication.

5x = 2(2x – 1)

5x = 4x – 2

5x – 4x = 2

x = 2

Problem 3 :       

(2x – 3)/(4x + 5) = 1/3

Solution :

(2x – 3)/(4x + 5) = 1/3

By doing on cross multiplication.

3(2x – 3) = 4x + 5

6x – 9 = 4x + 5

6x – 4x = 9 + 5

2x = 14

x = 14/2

x = 7

Problem  4  :

8/x = 5/(x – 1)

Solution :

8/x = 5/(x – 1)

By doing on cross multiplication.

8(x – 1) = 5x

8x – 8 = 5x

8x – 5x = 8

3x = 8

x = 8/3

Problem  5  :

[5(1 – x) + 3(1 + x)]/(1 – 2x) = 8 

Solution :

[5(1 – x) + 3(1 + x)]/(1 – 2x) = 8

Multiplying by (1-2x) on both sides, we get

5(1 – x) + 3(1 + x) = 8(1 – 2x)

5 – 5x + 3 + 3x = 8 – 16x

By combining the like terms.

-5x + 3x + 16x = 8 – 5 – 3

14x = 0

x = 0

Problem 6 :

[y – (4 – 3y)] / [2y – (3 + 4y)] = 1/5

Solution :

[y – (4 – 3y)] / [2y – (3 + 4y)] = 1/5

By doing on cross multiplication.

5(y – (4 – 3y) = 2y – (3 + 4y)

5(y – 4 + 3y) = 2y – 3 - 4y

5y – 20 + 15y = 2y – 3 – 4y

By combining the like terms.

5y + 15y – 2y + 4y = 20 – 3

22y = 17

y = 17/22

Problem 7 :

(9 – 3y)/(1 – 9y) = 8/5

Solution :

(9 – 3y)/(1 – 9y) = 8/5

By doing on cross multiplication.

5(9 – 3y) = 8(1 – 9y)

45 – 15y = 8 – 72y

Subtract  45 and add 15y on both sides.

45 – 15y – 8 + 72y = 0

37 + 57y = 0

57y = -37

y = -37/57

Problem 8 :

(3x + 2)/(2x – 3) = -3/4

Solution :

(3x + 2)/(2x – 3) = -3/4

By doing on cross multiplication.

4(3x + 2) = -3(2x – 3)

12x + 8 = -6x + 9

By combining the like terms.

12x + 6x = 9 – 8

18x = 1

x  = 1/18

Problem 9 :

(5x + 1)/(2x) = -1/3

Solution :

(5x + 1)/(2x) = -1/3

By doing on cross multiplication.

3(5x + 1) = -2x

15x + 3 = -2x

15x + 2x = -3

17x = -3

x = -3/17

Problem 10 :

(x + 1)/(2x + 7) = 3/8

Solution :

(x + 1)/(2x + 7) = 3/8

By doing on cross multiplication.

8(x + 1) = 3(2x + 7)

8x + 8 = 6x + 21

By combining the like terms.

8x – 6x = 21 - 8

2x = 13

x = 13/2

Problem 11 :

1/(x-1) + 2/(x+1) = 2

Solution :

1/(x-1) + 2/(x+1) = 2

Considering the denominators, they are not same. So, take least common multiple and make them same.

LCM = (x+1) (x-1)

[1/(x-1)] ∙ [(x+1)/(x+1)] + 2/(x+1) [(x-1)/(x-1)] = 2

[(x + 1)+2(x - 1)] / [(x - 1)(x + 1)] = 2

Multiplying (x-1) (x+1) on both sides.

(x + 1)  + 2(x - 1) = 2(x - 1)(x + 1)

Using distributive property.

x + 1 + 2x – 2 = 2(x² – 1)

By combining the like terms

3x – 1 = 2x² – 2

Subtract 3x and add 1 on both sides.

2x² – 3x – 2 + 1 = 0

2x² – 3x – 1 = 0

This quadratic equation is not factorable, using quadratic formula.

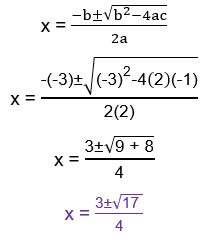
Problem 12 :

(50/x) + 4 = 14

Solution :

(50/x) + 4 = 14

By doing on cross multiplication with both sides.

(50 + 4x)/x = 14

50 + 4x = 14x

4x – 14x = -50

-10x = -50

x = 50/10

x = 5