SOLVING EQUATIONS OF DIFFERENT SOLUTION TYPES

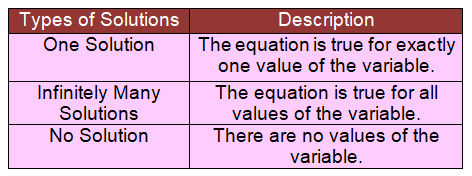
Determine if each equation has one solution, many solutions, or no solution. If the equation has a solution, determine the solution to the equation.

Problem 1 :

2x - x + 7 = x + 3 + 4

Solution :

 2x - x + 7 = x + 3 + 4

x + 7 =  x + 7

All real values will make the equation true. So, it has infinitely many solutions.  

Problem 2 :

-2(x + 1) = -2x + 5

Solution :

-2(x + 1) = -2x + 5

Distributing -2, we get

-2x – 2 = -2x + 5

No real values will satisfy the equation above. So, it has no solution.

Problem 3 :

4x + 2x + 2 = 3x - 7

Solution :

4x + 2x + 2 = 3x - 7

Combining the like terms, we get

6x + 2 = 3x - 7

Subtract 3x on both sides.

6x - 3x + 2 = 3x - 3x - 7

3x + 2 = -7

3x = -7 - 2

3x = -9

x = -9/3

x = -3

It has one solution or unique solution.

Problem 4 :

2(x + 2) + 3x = 2(x + 1) + 1

Solution :

2(x + 2) + 3x = 2(x + 1) + 1

Distributing 2, we get

2x + 4 + 3x = 2x + 2 + 1

Combining the like terms, we get

5x + 4 = 2x + 3

Subtract 2x on both sides.

 5x + 4 – 2x = 2x - 2x + 3

3x + 4 = 3

Subtract 3 on both sides.

3x + 4 – 3 = 3 – 3

3x + 1 = 0

3x = -1

x = -1/3

It has one solution or unique solution.

Problem 5 :

4(x - 1) = 1/2(x - 8)

Solution :

4(x - 1) = 1/2(x - 8)

Distributing 4 and 1/2, we get

 4x - 4 = x/2 – 4

Subtract x/2 on both sides.

4x - x/2 - 4 = x/2 - x/2 – 4

(8x - x)/2 – 4 = -4

(7x)/2 – 4 = -4

Add 4 on both sides.

(7x)/2 – 4 + 4 = -4 + 4

(7x)/2 = 0

x = 0

It has one solution or unique solution.

Problem 6 :

1/2(2 - 4x) + 2x = 13

Solution :

1/2(2 - 4x) + 2x = 13

Distributing 1/2, we get

(2)/2 - (4x)/2 + 2x = 13

1 – 2x + 2x = 13

1 = 13

No real values will satisfy the equation above. So, it has no solution.

Problem 7 :

3x - x + 4 = 4(2x - 1)

Solution :

3x - x + 4 = 4(2x - 1)

Distributing 4, we get

2x + 4 = 8x - 4

Subtract 8x on both sides.

2x + 4 – 8x = 8x - 4 – 8x

-6x + 4 = -4

Add 4 on both sides.

-6x + 4 + 4 = -4 + 4

-6x + 8 = 0

-6x = -8

x = 4/3

It has one solution or unique solution.

Problem 8 :

4(2x + 1) = 5x + 3x + 9

Solution :

4(2x + 1) = 5x + 3x + 9

Distributing 4, we get

8x + 4 = 5x + 3x + 9

8x + 4 = 8x + 9

No real values will satisfy the equation above. So, it has no solution.

Problem 9 :

10 + x = 5(1/5x + 2)

Solution :

10 + x = 5(1/5x + 2)

Distributing 5, we get

10 + x = (5x)/5 + 10

10 + x = x + 10

All real values will make the equation true. So, it has infinitely many solution.

Problem 10 :

8(x + 2) = 2x + 16

Solution :

8(x + 2) = 2x + 16

Distributing 8, we get

8x + 16 = 2x + 16

Subtract 2x on both sides.

8x + 16 - 2x = 2x - 2x + 16

6x + 16 = 16

Subtract 16 on both sides.

6x + 16 - 16 = 16 - 16

6x = 0

x = 0

It has one solution or unique solution.

Problem 11 :

3 + 3/2x + 4 = 4x - 5/2x

Solution :

3 + 3/2x + 4 = 4x - 5/2x

Combining the like terms, we get

7 + 3/2x = (8x – 5x)/2

7 + 3/2x = 3/2x

No real values will satisfy the equation above. So, it has no solution.