SOLVING CUBIC POLYNOMIAL EQUATIONS

Problem 1 :

Solving x³ + 9x² - x - 9 = 0 we get the following roots

(a) ± 1,-9     (b) ±1, ±9      (c) ±1, 9      (d) None

Solution :

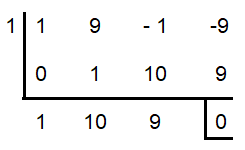
So, factors are (x - 1)(x² + 10x + 9).

x² + 10x + 9 = (x + 1) (x + 9)

Equating each factor to zero, we get

x + 1 = 0    x - 1 = 0        x + 9 = 0

x = -1, 1 and 9.

Problem 2 :

The solution of the cubic equation x³ - 6x² + 11 x - 6 = 0 is given by the triplet

(a) (-1, 1, -2)    (b) (1, 2, 3)      (c) (-2, 2, 3)     (d) (0, 4, -5)

Solution :

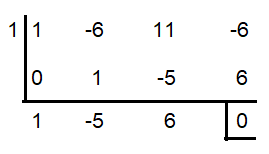
So, the factors are (x - 1) (x² - 5x + 6)

x² - 5x + 6 = (x - 2) (x - 3)

Equating each factor to zero, we get

x - 1 = 0       x - 2 = 0       x - 3 = 0

x = 1, 2 and 3

Problem 3 :

For the given polynomial 

x³ - 2x² - 5x + 6

If 3 is one of the zeroes, find the others.

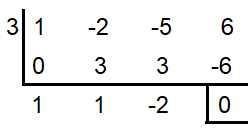
writing the left over as quadratic polynomial, we get

x² + x - 2

To get the other factors,

x² + x - 2 = 0

(x + 2) (x - 1) = 0

x = -2 and x = 1

So, the three zeroes are -2, 1 and 3.

Problem  4 :

Is x = 4 a root of the equation x³ − 6x² + 9x + 1 = 0?

Solution :

Let p(x) = x³ − 6x² + 9x + 1

To check if x = 4 is a factor, we will use remainder theorem. If the remainder is 0, then 4 is a factor otherwise it is not.

p(4) = 4³ − 6(4)² + 9(4) + 1

p(4) = 64 − 96 + 36 + 1

p(4) = 101 - 96

p(4) = 5

So, 4 is not a root of the polynomial.

Problem 5 :

Find a polynomial function P(x) of degree 3 with real coefficients that satisfies the given conditions.

Zeros of -3, -1, and 4; P(2) = 5

Solution :

Zeroes of the cubic polynomial are -3, -1 and 4.

x = -3, x = -1 and x = 4

Factors are (x + 3)(x + 1) (x - 4).

Multiplying the factors, we get

p(x) = k (x + 3)(x + 1) (x - 4)

p(x) = k (x² + 4x + 3)(x - 4)

p(x) = k (x³ - 4x² + 4x² - 16x + 3x - 12)

p(x) = k (x³ - 13x - 12) 

P(2) = 5

From the given information, the cubic polynomial should satisfy the condition P(2) = 5

p(2) = k (2³ - 13(2) - 12)

5 = k(8 - 26 - 12)

5 = k(-30)

-5/30 = k

k = -1/6