SOLVING CUBIC EQUATION

Problem 12 :

The rational root of the equation 2x³ - x² - 4x + 2 = 0 is 

(a) 1/2    (b) -1/2    (c)  2    (d)  -2

Solution :

2x³ - x² - 4x + 2 = 0

x² (2x - 1) - 2(2x - 1) = 0

(x² - 2)(2x - 1) = 0

x² - 2 = 0 and 2x - 1 = 0

x² = 2 and x = 1/2

So, the roots are x = √2, -√2 and 1/2. Option a.

Problem 13 :

The satisfying value of x³ + x² - 20x = 0 are

(a) (1, 4, -5)    (b) (2, -4,-5)   (c)  (0, -4, 5)    (d)  (0, 4, -5)

Solution :

x³ + x² - 20x = 0

x(x² + x - 20) = 0

x(x + 5)(x - 4) = 0

Equating each factor to 0, we get

x = 0, x + 5 = 0 and x - 4 = 0

x = 0, x = -5 and x = 4

So, the solution is (-5, 0, 4), option d.

Problem 14

Solve x³ - 6x² + 5x + 12 = 0 given that the product of two roots is 12

(a) (1, 3, 4)    (b) (-1,3 ,4)   (c)  (1,6,2 )    (d)  (1, -6, -2)

Solution :

x³ - 6x² + 5x + 12 = 0

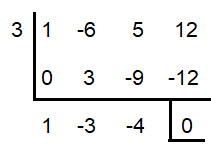
x² - 3x - 4 = 0

(x - 4) (x + 1) = 0

x = 4 and x = -1

So, the roots are 3, -1 and 4.

Problem 15 :

When √(2z + 1) + √(3z + 4) = 7 the value of z is given by

(a) 1    (b) 2   (c)  3    (d)  4

Solution :

So, the answer is option d.