SOLVING ABSOLUTE VALUE INEQUALITIES GRAPHICALLY

The absolute value inequality which is in the form of

|ax + b| < c, |ax + b| ≤ c, |ax + b| > c or |ax + b| ≥ c

can be decomposed into two branches.

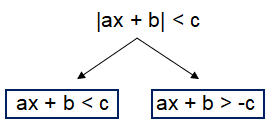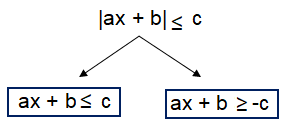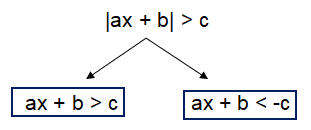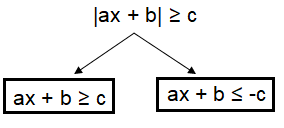Then we will solve those two branches separately and find the values of unknown.

To represent the solution in the number line, we will use two types of circles.

Solid circle (or) filled circle
Transparent circle (or) empty circle

In the inequality, if we have ≥ or ≤ then we have to use solid circle.

In the inequality, if we have < or > then we have to use empty circle.

Solve the inequality. Then graph the solution.

Problem 1 :

|d + 4| ≥ 3

Solution :

|d + 4| ≥ 3

d + 4 ≥ 3

d ≥ 3 – 4

d ≥ -1

d + 4 ≤ -3

d ≤ -3 - 4

d ≤ -7

Converting into interval notation, we get

(-∞, -7] U [-1, ∞)

Problem 2 :

|f + 6| < 2

Solution :

|f + 6| < 2

f + 6 < 2

f < 2 – 6

f < -4

f + 6 > -2

f > -2 – 6

f > -8

Converting the shaded portion as interval notation, we get

(-8, -4)

Problem 3 :

|3w - 15| < 30

Solution :

|3w - 15| < 30

3w - 15 < 30

3w < 30 + 15

3w < 45

w < 45/3

w < 15

3w - 15 > -30

3w > -30 + 15

3w > -15

w > -15/3

w > -5

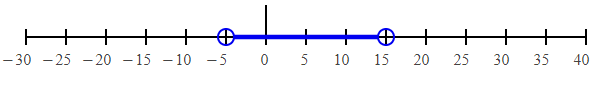
Converting the shaded region as interval notation, we get

(-5, 15).

Problem 4 :

|2x + 6| ≥ 10

Solution :

|2x + 6| ≥ 10

2x + 6 ≥ 10

2x ≥ 10 – 6

2x ≥ 4

x ≥ 4/2

x ≥ 2

2x + 6 ≤ -10

2x ≤ -10 – 6

2x ≤ -16

x ≤ -16/2

x ≤ -8

Converting into interval notation, we get

(-∞, -8] U [2, ∞)

Problem 5 :

|16 - p| > 3

Solution :

|16 - p| > 3

16 - p > 3

- p > 3 – 16

-p > -13

p > 13

16 - p < -3

-p < -3 – 16

-p < -19

p < 19

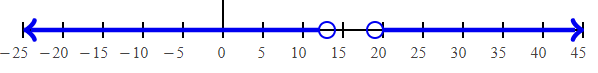
Converting into interval notation, we get

(-∞, 13) U [19, ∞)

Problem 6 :

|24 - q| ≤ 11

Solution :

|24 - q| ≤ 11

24 - q ≤ 11

-q ≤ 11 – 24

-q ≤ -13

q ≤ 13

24 – q ≥ -11

-q ≥ -11 – 24

-q ≥ -35

q ≥ 35

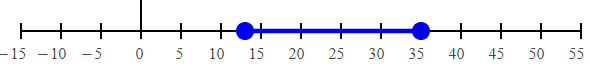
Converting into interval notation, we get

(13, 35]

Problem 7 :

|1/2x - 10| ≤ 4

Solution :

|1/2x - 10| ≤ 4

1/2x – 10 ≤ 4

1/2x ≤ 4 + 10

1/2x ≤ 14

x ≤ 14 × 2

x ≤ 28

1/2x – 10 ≥ -4

1/2x ≥ -4 + 10

1/2x ≥ 6

x ≥ 6 × 2

x ≥ 12

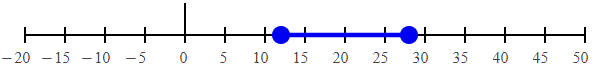
Converting into interval notation, we get

[12, 28]

Problem 8 :

|(1/3)m - 15| < 6

Solution :

|(1/3)m - 15| < 6

(1/3)m - 15 < 6

(1/3)m < 6 + 15

(1/3)m < 21

m < 21 × 3

m < 63

(1/3)m - 15 > -6

(1/3)m > -6 + 15

(1/3)m > 9

m > 9 ×3

m > 27

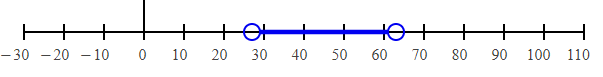
Converting into interval notation, we get

(27, 63)

Problem 9 :

|(1/7)y + 2| - 5 > 3

Solution :

|(1/7)y + 2| - 5 > 3

|(1/7)y + 2| > 3 + 5

|(1/7)y + 2| > 8

(1/7)y + 2 > 8

(1/7)y > 8 – 2

(1/7)y > 6

y > 6 × 7

y > 42

(1/7)y + 2 < -8

(1/7)y < -8 – 2

(1/7)y < -10

y < -10 × 7

y < -70

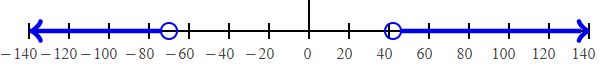
Converting into interval notation, we get

(-∞, -70) U (42, ∞)

Problem 10 :

|(2/5)n - 8| + 4 ≥ 12

Solution :

|2/5n - 8| + 4 ≥ 12

|2/5n – 8| ≥ 12 - 4

|2/5n – 8| ≥ 8

(2/5)n – 8 ≥ 8

(2/5)n ≥ 8 + 8

(2/5)n ≥ 16

n ≥ 16 × 5/2

n ≥ 40

(2/5)n – 8 ≤ -8

(2/5)n ≤ -8 + 8

(2/5)n ≤ 0

n ≤ 0

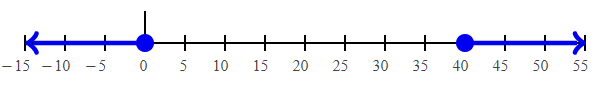
Converting into interval notation, we get

(-∞, 0] U [40, ∞)

SOLVING ABSOLUTE VALUE INEQUALITIES GRAPHICALLY

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling