SOLVING ABSOLUTE VALUE EQUATIONS GRAPHICALLY

The point of intersections of absolute value functions will be the solution. To find the point of intersection from the graph, first we should know how to draw the graph of absolute value function.

Always absolute value function will create the shape of V.

Vertex :

Vertex of the absolute value function will denote where the curve will start.

By comparing the given absolute value function with

y = a|x - h| + k, we can draw the graph easily.

Here (h, k) is vertex. Sign of a represents the direction of opening.

Solve for x using

i) graphical method ii) an algebraical method.

Problem 1 :

|x + 2| = 2x + 1

Solution :

Graphing absolute value equation :

Let y = |x + 2| = 2x + 1

y = |x + 2| and y = 2x + 1

Comparing y = |x + 2| with y = a|x - h| + k

(h, k) is (-2, 0). a = 1, the curve is opening up.

By applying x = 0, we get y = 2. So, (0, 2) is the y-intercept.

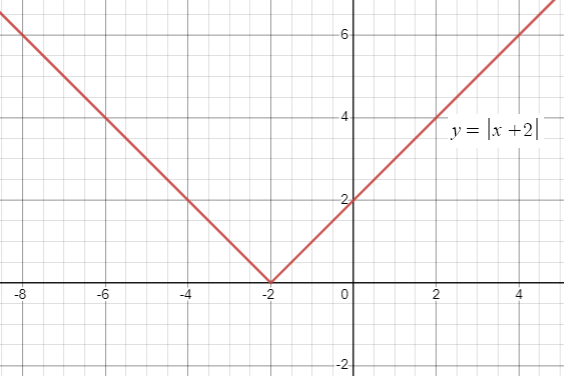
Graphing the line :

y = 2x + 1

Slope (m) = 2

x-intercept :

Put y = 0

y = 2x + 1

2x + 1 = 0

2x = -1

x = -1/2

(-1/2, 0)

y-intercept :

Put x = 0

y = 2(0) + 1

y = 0 + 1

y = 1

(0, 1)

It is a raising line.

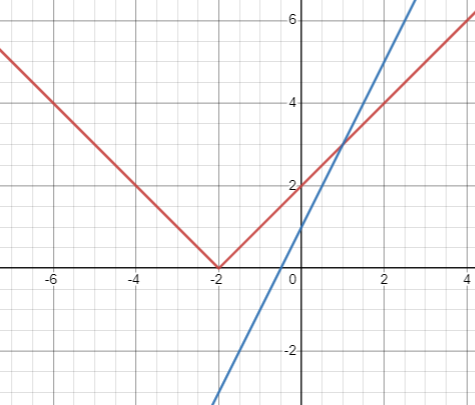
Tracing the next point after y-intercept of absolute value function, we land at (1, 3).

Using slope, we can find the next point on the line. From 1 on the y-axis move 2 units above and 1 unit to the right. We will be landing on the point (1, 3). So, the solution is (1, 3).

Solving algebraically :

|x + 2| = 2x + 1

x + 2 = (2x + 1)

x + 2 = 2x + 1

x - 2x = 1 - 2

-x = -1

x = 1

(x + 2) = -(2x + 1)

x + 2 = -2x - 1

x + 2x = -1 - 2

-3x = 3

x = -1

Considering the x - intercepts of the line and absolute value function, we should take the value of x as 1.

Applying the value of x in the original function, we will get y = 3.So, (1, 3) is the point of intersection.

SOLVING ABSOLUTE VALUE EQUATIONS GRAPHICALLY

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling