SOLVING ABSOLUTE VALUE EQUATIONS BY GRAPHING

The point of intersection of absolute value functions is known as solution.

Always absolute value function will create the shape of V.

Vertex :

Vertex of the absolute value function will denote where the curve will start.

By comparing the given absolute value function with

y = a|x - h| + k, we can draw the graph easily.

Here (h, k) is vertex. Sign of "a" represents the direction of opening.

Solve each equation by graphing a system.

Problem 1 :

|x + 3| = 2

Solution :

Let y = |x + 3| and y = 2

Comparing y = |x + 3| with y = a|x - h| + k, we get

(h, k) ==> (-3, 0)

Tracing some more points,

If x = -6, y = |-6 + 3| = 3

If x = -5, y = |-5 + 3| = 2

If x = -4, y = |-4 + 3| = 1

If x = -2, y = |-2 + 3| = 1

If x = -1, y = |-1 + 3| = 2

If x = 0, y = |0 + 3| = 3

(-6, 3)

(-5, 2)

(-4, 1)

(-2, 1)

(-1, 2)

(0, 3)

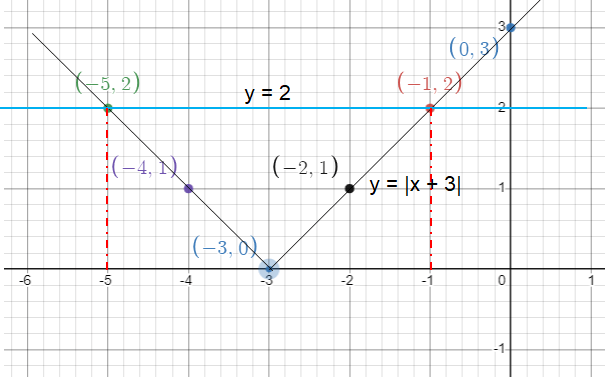
So, solutions are -5 and -1.

Problem 2 :

|x - 3| = 1

Solution :

Let y = |x - 3| and y = 1

Comparing y = |x - 3| with y = a|x – h| + k, we get

(h, k) = (3, 0)

Tracing some more points,

If x = 1, y = |1 – 3| = 2

If x = 2, y = |2 – 3| = 1

If x = 4, y = |4 – 3| = 1

If x = 5 y = |5 – 3| = 2

(1, 2)

(2, 1)

(4, 1)

(5, 2)

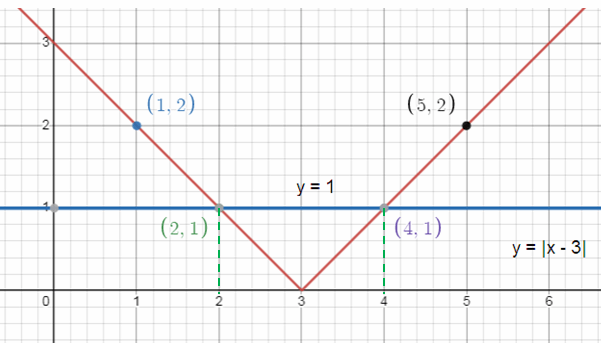
So, solutions are x = 2 and x = 4.

Problem 3 :

|x + 1| = 1

Solution :

Let y = |x + 1| and y = 1

Comparing y = |x + 1| with y = a|x – h| + k, we get

(h, k) = (-1, 0)

Tracing some more points,

If x = 0, y = |0 + 1| = 1

If x = -2, y = |-2 + 1| = 1

If x = -3, y = |-3 + 1| = 2

If x = -4, y = |-4 + 1| = 3

(0, 1)

(-2, 1)

(-3, 2)

(-4, 3)

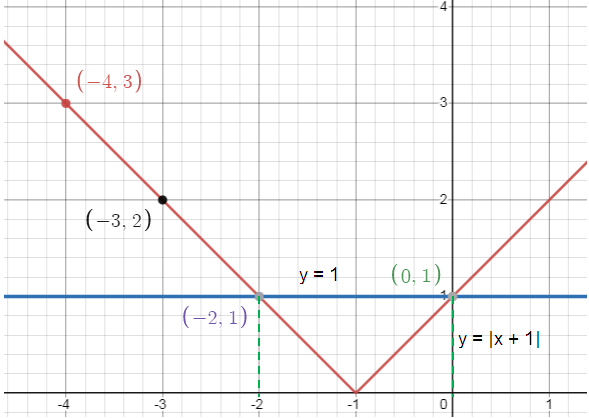
So, solutions are x = -2 and x = 0.

Problem 4 :

|1 + x| = 3

Solution :

Let y = |1 + x| and y = 3

Comparing y = |x - (-1)| with y = a|x – h| + k, we get

(h, k) = (-1, 0)

Tracing some more points,

If x = 0, y = |1 + 0| = 1

If x = -2, y = |1 - 2| = 1

If x = -3, y = |1 - 3| = 2

If x = -4, y = |1 - 4| = 3

If x = 0, y = |1 + 0| = 1

If x = 1, y = |1 + 1| = 2

If x = 2, y = |1 + 2| = 3

(0, 1)

(-2, 1)

(-3, 2)

(-4, 3)

(0, 1)

(1, 2)

(2, 3)

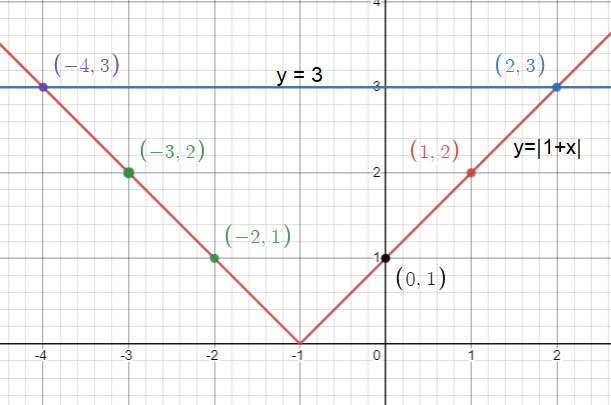
So, solutions are x = -2 and x = 0.

Problem 5 :

3|x – 2| + 3 = 6

Solution :

3|x – 2| + 3 = 6

3|x – 2| = 6 – 3

3|x – 2| = 3

|x – 2| = 3/3

|x – 2| = 1

Let y = |x - 2| and y = 1

Comparing y = |x - 2| with y = a|x – h| + k, we get

(h, k) = (2, 0)

Tracing some more points,

If x = 1, y = |1 – 2| = 1

If x = 3, y = |3 – 2| = 1

If x = 4, y = |4 – 2| = 2

If x = 5 y = |5 – 2| = 3

(1, 1)

(3, 1)

(4, 2)

(5, 3)

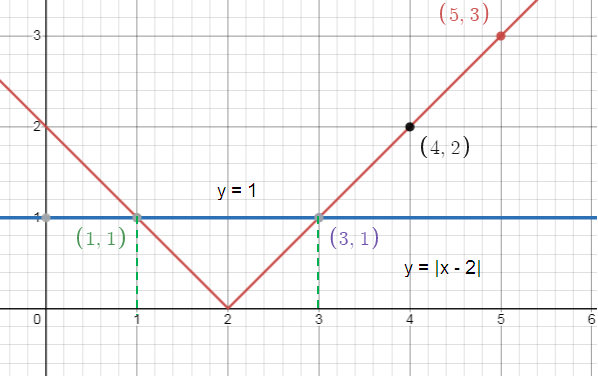
So, solutions are x = 1 and x = 3.

Problem 6 :

3 - 4|x - 1| = -1

Solution :

3 - 4|x - 1| = -1

- 4|x - 1| = -1 – 3

-4|x – 1| = -4

|x – 1| = -4/-4

|x – 1| = 1

Let y = |x - 1| and y = 1

Comparing y = |x - 1| with y = a|x – h| + k, we get

(h, k) = (1, 0)

Tracing some more points,

If x = 0, y = |0 – 1| = 1

If x = 2, y = |2 – 1| = 1

If x = 3, y = |3 – 1| = 2

If x = 4 y = |4 – 1| = 3

(0, 1)

(2, 1)

(3, 2)

(4, 3)

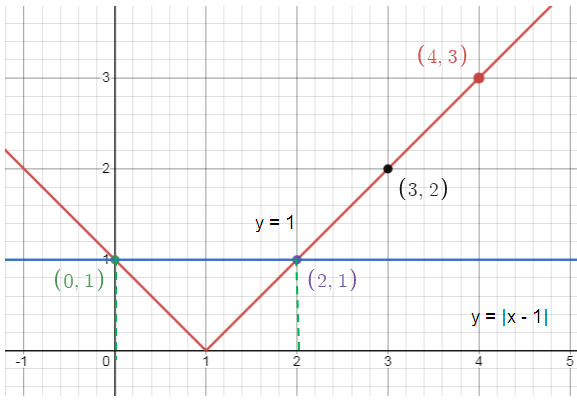
So, solutions are x = 0 and x = 2.

Problem 7 :

4 + |x + 1| = 5

Solution :

4 + |x + 1| = 5

|x + 1| = 5 – 4

|x + 1| = 1

Let y = |x + 1| and y = 1

Comparing y = |x + 1| with y = a|x – h| + k, we get

(h, k) = (-1, 0)

Tracing some more points,

If x = 0, y = |0 + 1| = 1

If x = -2, y = |-2 + 1| = 1

If x = -3, y = |-3 + 1| = 2

If x = -4, y = |-4 + 1| = 3

(0, 1)

(-2, 1)

(-3, 2)

(-4, 3)

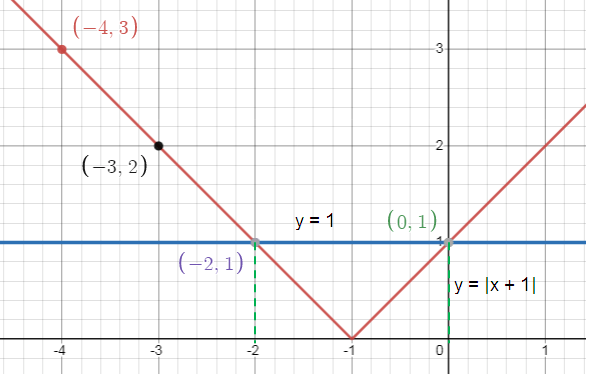
So, solutions are x = -2 and x = 0.

Problem 8 :

2|x + 2| + 3 = 5

Solution :

2|x + 2| + 3 = 5

2|x + 2| = 5 – 3

2|x + 2| = 2

|x + 2| = 2/2

|x + 2| = 1

Let y = |x + 2| and y = 1

Comparing y = |x + 2| with y = a|x – h| + k, we get

(h, k) = (-2, 0)

Tracing some more points,

If x = 0, y = |0 + 2| = 2

If x = -1, y = |-1 + 2| = 1

If x = -3, y = |-3 + 2| = 1

If x = -4, y = |-4 + 2| = 2

(0, 2)

(-1, 1)

(-3, 1)

(-4, 2)

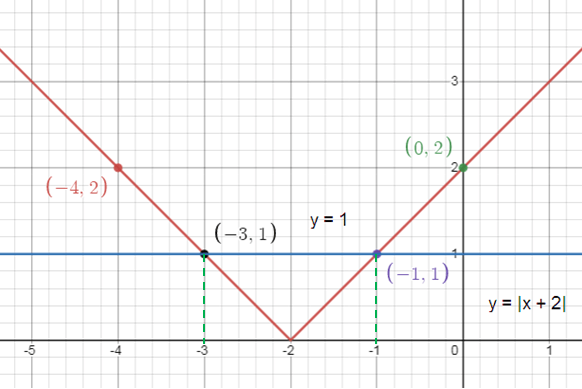
So, solutions are x = -3 and x = -1.

SOLVING ABSOLUTE VALUE EQUATIONS BY GRAPHING

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling