SOLVE USING PROPERTIES OF INVERSE TRIGONOMETRIC FUNCTIONS

Find the value, if it exists. If not, give the reason for non existence.

Problem 1 :

sin^-1(cos π)

Solution :

= sin^-1(cos π)

Evaluating cos π, we get -1

= sin^-1(-1)

Since it is sin function, the principal solution must lie in between [-π/2, π/2]

sin^-1(-1) = - sin(1) ==> -π/2

General solution :

= nπ+(-1)ⁿ α

Here α = -π/2

Applying the value of α, we get

= nπ+(-1)ⁿ (-π/2)

Problem 2 :

tan^-1 (sin (-5π/2))

Solution :

= tan^-1 (sin (-5π/2))

Let us evaluate sin (-5π/2) first.

sin (-5π/2) = - sin (5π/2)

= - sin (π + 3π/2)

In 3rd quadrant, for tangent and its reciprocal cotangent for these two trigonometric ratios we have positive sign.

=  sin (3π/2)

= -1

By applying sin (-5π/2) = -1, we get

= tan^-1 (-1)

For what angle measure of tangent, we get 1.

Since it is tangent function, the principal solution should lie in between (-π/2, π/2)

tan^-1 (-1) = -π/4

General solution :

= nπ+ α

Here α = -π/4

= nπ + (-π/4)

Problem 3 :

sin^-1 (sin 5)

Solution :

= sin^-1 (sin 5)

Since 5 > 1, we reduce the value by subtracting it with 2π.

= sin^-1 (sin (5 - 2π))

= (5 - 2π)

Find the value of the expression in terms of x, with the help of a reference triangle.

Problem 4 :

sin (cos^-1(1 - x))

Solution :

cos^-1(1 - x)

Adjacent side = 1 - x, hypotenuse = 1

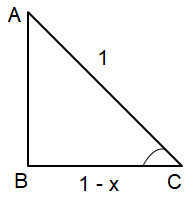opposite side = √12 - (1 - x)2 = √12 - (1 - 2x + x2) = √(1 - 1 + 2x - x2) Opposite side = √(2x - x2)

sin (cos^-1(1 - x)) = sin (sin^-1 (√(2x - x²))

= √(2x - x²)

Problem 5 :

cos (tan^-1(3x - 1))

Solution :

tan^-1(3x - 1)

Opposite side = 3x- 1, adjacent side = 1

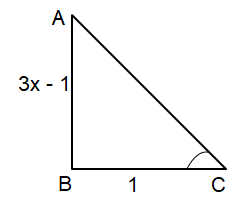Hypotenuse = √(3x - 1)2 + 12 = √(9x2 - 6x + 1 + 12) = √(9x2 - 6x + 2)

cos (tan^-1(3x - 1)) = cos (cos^-1(1/√(9x² - 6x + 2))

= 1/√(9x² - 6x + 2)

Problem 6 :

tan (sin^-1(x + 1/2))

Solution :

tan (sin^-1(x + 1/2))

= tan ( sin^-1(2x + 1)/2 )

Opposite side = 2x + 1, Hypotenuse = 2

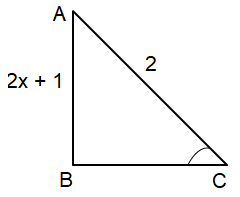Adjacent side = √(22 - (2x + 1)2 = √(4 - (4x2 + 4x + 1) = √(4 - 4x2 - 4x - 1) = √(3 - 4x2 - 4x)

Adjacent side = √(3 - 4x - 4x²)

= tan ( tan^-1(2x + 1)/√(3 - 4x - 4x²) )

= (2x + 1)/√(3 - 4x - 4x²)