SOLVE THE CUBIC EQUATION WITH GIVEN INFORMATION ABOUT ROOTS

Problem 1 :

Solve the equation

3x³ - 16x² + 23x - 6 =0

if the product of two roots is 1.

Solution :

Let the roots be α, β and γ

Sum of the roots = α + β + γ = -b/a

Here a = 3, b = -16, c = 23 and d = -6

α + β + γ = -(-16)/3

α + β + γ = 16/3 ----(1)

Product of the roots = α β γ

α β γ = -d/a

1(γ) = 6/3

γ = 2

α β = 1

β = 1/α

Applying the value of β and γ = 2 in (1), we get

α + 1/α + 2 = 16/3

(α² + 1)/α = (16/3) - 2

(α² + 1)/α = 10/3

3(α² + 1) = 10α

3α² + 3 = 10α

3α² - 10α + 3 = 0

(3α - 1) (α - 3) = 0

The roots are 1/3, 3 and -2 (or) 3, 1/3, -2

Problem 2 :

Find the sum of the square of roots of the equation

2x⁴ - 8x³ + 6x² - 3 = 0

Solution :

By comparing the given cubic equation with

ax³ + bx² + cx + d = 0

a = 2, b = -8, c = 6 ad d = -3

Sum of the roots = α + β + γ = -b/a

α + β + γ = 8/2 ==> 4

Sum of product of its two roots :

α β + βγ + γα = c/a

α β + βγ + γα = 3

α² + β² + γ² = (α + β + γ)² - 2(α β + βγ + γα)

α² + β² + γ² = (4)² - 2(3)

= 16 - 6

α² + β² + γ² = 10

Problem 3 :

Solve the equation 

x³ - 9x² + 14x + 24 = 0

if it is given that two of its roots are in the ratio 3 : 2.

Solution :

Let the roots be α, β and γ

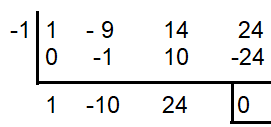
x = -1 is one of the solution, the remaining two solutions can be found by solving the quadratic equation.

x² - 10x + 24 = 0

(x - 4)(x - 6) = 0

x = 4 and x = 6

So, the solutions are -1, 4 and 6.

Note : 

Here the roots 6 and 4 is in the ratio 3 : 2.

Problem 4 :

If  α, β and γ are the roots of the polynomial equation

ax³ + bx² + cx + d = 0

find the value of Σα/βγ in terms of the coefficients.

Solution :

Problem 5 :

If  α, β, γ and δ are the roots of the polynomial equation

2x⁴ + 5x³ - 7x² + 8 = 0

find a quadratic equation with integer coefficients whose roots are α + β + γ + δ and α β γ δ.

Solution :

2x⁴ + 5x³ - 7x² + 8 = 0

Comparing the given polynomial of highest exponent 4 with

ax⁴ + bx³ + cx² + dx + e = 0

a = 2, b = 5, c = -7, d = 0 and e = 8

and roots of the above polynomial are α, β, γ and δ.

Sum of roots (α + β + γ + δ) = -b/a

(α + β + γ + δ) = -5/2

Product of roots α β γ δ = e/a

α β γ δ = 8/2 ==> 4

Sum of roots of new equation :

(α + β + γ + δ) + α β γ δ = (-5/2) + 4 

= 3/2

Product of roots of new equation :

(α + β + γ + δ) x α β γ δ = (-5/2) x 4 

= -10

The new equation will be

x² - (3/2)x + (-10) = 0

2x² - 3x - 20 = 0