SOLVE SYSTEMS OF EQUATIONS BY GRAPHING
What is solution in systems of linear equations ?
The point of intersection is known as solution. In general , two lines may meet at a point, they meet at infinitely many points, they will never meet.
- If two lines are intersecting at one point, there is unique solution.
- If two lines are parallel, they will never meet. So no solution.
- If two lines are coincident, then they will touch each other at infinite number of points. So, infinitely many solutions.
To draw the graph of the line, we have different ways. Here we follow of finding intercepts and drawing the graph.
Find the simultaneous solution of the following pairs of equations using graphical methods:
Problem 1 :
y = 3x - 1
y = 2x - 2
Solution :
y = 3x - 1
|
x-intercept : y = 3x - 1 Put y = 0 3x - 1 = 0 3x = 1 x = 1/3 (1/3, 0) |
y-intercept : y = 3x - 1 Put x = 0 y = 3(0) - 1 y = -1 (0, -1) |
By connecting these two points, we get the first line.
y = 2x - 2
|
x-intercept : y = 2x - 2 Put y = 0 2x - 2 = 0 2x = 2 x = 1 (1/3, 0) |
y-intercept : y = 2x - 2 Put x = 0 y = 2(0) - 2 y = -2 (0, -2) |
By connecting these two points, we get the second line.
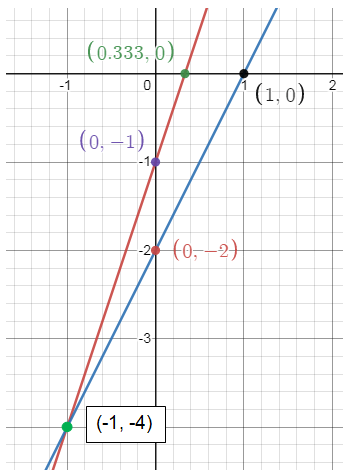
In the graph, the lines are intersecting at a point (-1, -4).
So, the solution is (-1, -4).
Problem 2 :
y = -2x + 3
y = x + 6
Solution :
y = -2x + 3
|
x-intercept : y = -2x + 3 Put y = 0 -2x + 3 = 0 -2x = -3 x = 3/2 (3/2, 0) |
y-intercept : y = -2x + 3 Put x = 0 y = -2(0) + 3 y = 3 (0, 3) |
By connecting these two points, we get the graph of the first line.
|
x-intercept : y = x + 6 Put y = 0 x + 6 = 0 x = -6 (-6, 0) |
y-intercept : y = x + 6 Put x = 0 y = 0 + 6 y = 6 (0, 6) |
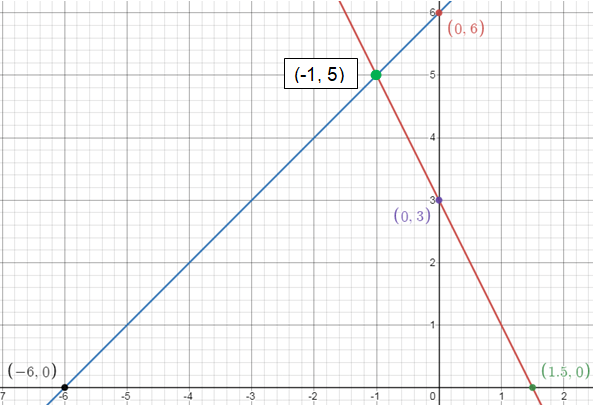
So, the solution is (-1, 5).
Problem 3 :
y = -(4/3)x + 1
x = 3
Solution :
y = -(4/3) x + 1
|
x-intercept : y = -(4/3) x + 1 Put y = 0 -(4/3)x + 1 = 0 -(4/3)x = -1 x = 3/4 (3/4, 0) |
y-intercept : y = -(4/3) x + 1 Put x = 0 y = -(4/3)(0) + 1 y = 1 (0, 1) |
By connecting the points (3/4, 0) and (0, 1), we get the graph of the first line.
The second line is x = 3, it is vertical line passes through 3 on the x-axis.
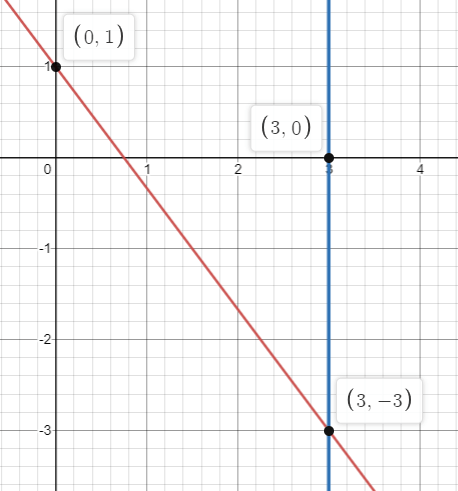
So, (3, -3) is the solution.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling