SOLVE FOR UNKNOWN IN RHOMBUS INVOLVING SIDE LENGTH

 Find the value of x in each rhombus.

Problem 1 :

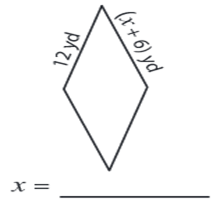
Solution :

Side length = 12 yd and (x + 6) yd

We know that all the sides are equal in a rhombus.

x + 6 = 12

x = 12 - 6

x = 6

Problem 2 :

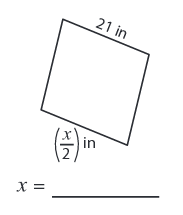
Solution :

Given, side length = 21 in and (x/2) in

We know that all the sides are equal in a rhombus.

x/2 = 21

x = 21 × 2

x = 42

Problem 3 :

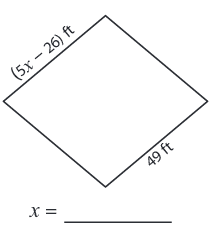
Solution :

Side length are 49 ft and (5x - 26) ft

We know that all the sides are equal in a rhombus.

5x - 26 = 49

5x = 49 + 26

5x = 75

x = 15

Problem 4 :

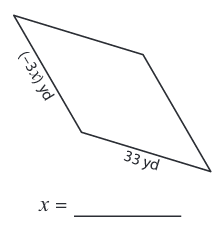
Solution :

Side length = 33 yd and (-3x) yd

We know that all the sides are equal in a rhombus.

-3x = 33

x = -33/3

x = -11

Find the value of x and y in each rhombus.

Problem 5 :

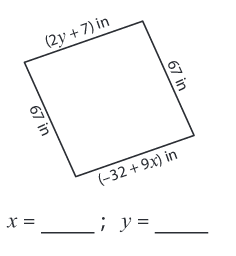
Solution :

Given, side length = (2y + 7) in, 67 in, (-32 + 9x) in and 67 in

We know that all the sides are equal in a rhombus.

So, x = 11 and y = 30.

Problem 6 :

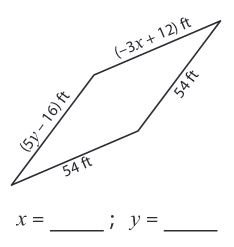
Solution :

Side lengths are (5y - 16) ft, 54 ft, (-3x + 12) ft and 54 ft

We know that all the sides are equal in a rhombus.

So, x = -14 and y = 14.

Problem 7 :

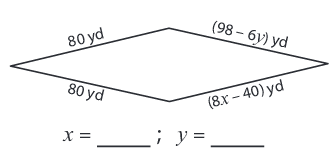
Solution :

Side lengths are (98 - 6y) yd, 80 yd, (8x - 40) yd and 80 yd

We know that all the sides are equal in a rhombus.

So, x = 15 and y = 3.

Problem 8 :

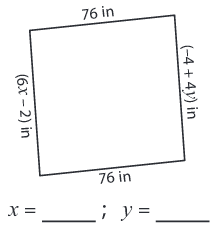
Solution :

Side lengths are (6x - 2) in, 76 in, (-4 + 4y) in and 76 in

We know that all the sides are equal in a rhombus.

So, x = 13 and y = 20.