SLOPES OF PARALLEL AND PERPENDICULAR LINES

Parallel lines :

Parallel lines will have the same slope.

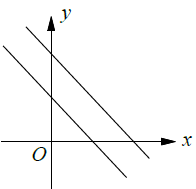
If m₁ and m₂ are slopes of the 1^st and 2^nd line, then

m₁ = m₂

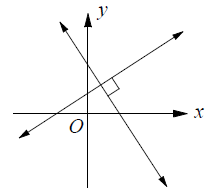
Perpendicular Lines :

Lines that intersect at right angles are called perpendicular lines.

If the product of the slopes of two nonvertical lines is -1, then the lines are perpendicular

Problem 1 :

In the xy plane, the lines

y = mx - 7 are 2x + 3y = 6

are parallel. What is the value of m ?

Solution :

Slope of the line y = mx - 7 :

By comparing the given equation with slope intercept form

y = mx + b

m₁ = m

Slope of the line 2x + 3y = 6 :

3y = -2x + 6

Dividing by 3 on both sides.

y = (-2/3) x + (6/3)

y = (-2/3) x + 2

m₂ = -2/3

Since the given lines are parallel,

m₁ = m₂

m = -2/3

Problem 2 :

A line passes through the points (-1, 2) and (5, b) and is parallel to the graph of the equation 4x - 2y = 13. What is the value of b ?

Solution :

Slope of the line joining the points (-1, 2) and (5, b).

m = (y₂ - y₁) / (x₂ - x₁)

m₁ = (b - 2) / (5 + 1)

m₁ = (b - 2) / 6 ---(1)

4x - 2y = 13

2y = 4x - 13

Dividing by 2 on both sides.

y = (4x/2) - (13/2)

y = 2x - (13/2)

m₂ = 2 ----(2)

(1) = (2)

(b - 2) / 6 = 2

Multiply by 6 on both sides.

b - 2 = 12

Add 2 on both sides.

b = 12 + 2

b = 14

Problem 3 :

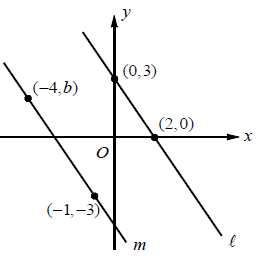
In the xy - plane above, line l is parallel to line m. What is the value of b?

Solution :

The line (m) passes through the points (-1, -3) and (-4, b)

The line (l) passes through the points (2, 0) and (0, 3)

m = (y₂ - y₁)/(x₂ -x₁)

Since the lines are parallel m₁ = m₂

(b + 3) / (-3)  =  -3/2 

Doing cross multiplication, we get

2(b + 3) = -3(-3)

2b + 6 = 9

2b = 9 - 6

2b = 3

Dividing by 2 on both sides.

b = 3/2

Problem 4 :

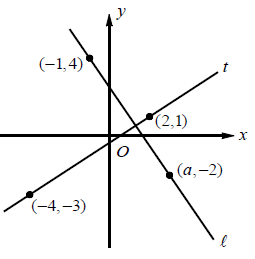
In the xy-plane above, if line l is perpendicular to line t, what is the value of a?

Solution :

The line (t) passes through the points (-4, -3) and (2, 1).

The line (l) passes through the points (a, -2) and (-1, 4).

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

2/3 = 6/(a - 1)

Doing cross multiplication, we get

2(a - 1) = 6(3)

2a - 2 = 18

Add 2 on both sides.

2a = 20

a = 10