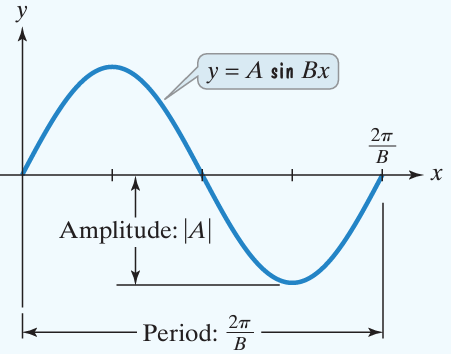
SKETCHING THE GRAPH OF Y EQUAL A SIN BX
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To learn how to sketch the graph of y = A sin Bx, we have to understand the meaning of the terms involving this topic.
- The amplitude is the vertical distance between a maximum or minimum point of the principal axis. From the given equation, A is amplitude.
- The horizontal length of one cycle of the graph is known as period. To calculate period, we will use the formula 2𝜋/|B|
- For the function in the form y = A sin Bx, there is no horizontal or vertical shift.
In general for the function y = sin x.
- Amplitude is 1 and period is 2𝜋.
- the graph will start with (0, 0).
- To get the next inputs, we will add the preceding inputs by the value of period / 4
Determine the amplitude, period, phase shift of each function. Then graph of one period of the function.
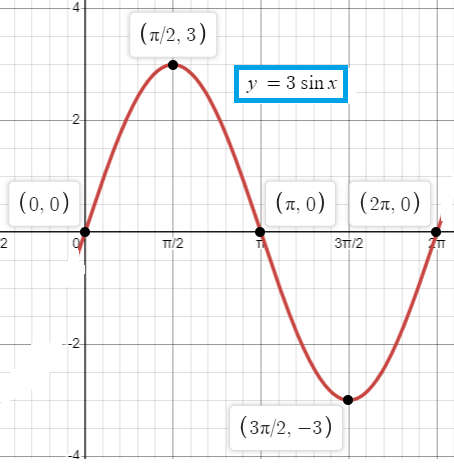
Problem 1 :
y = 3 sin x
Solution :
Comparing the given function with y = A sin Bx
y = 3 sin x
A = 3, B = 1
Finding amplitude :
Amplitude = 1
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= 2𝜋/4
= 𝜋/2
Calculating Inputs and Outputs :
|
x = 0 y = 3 sin 0 y = 0 |
x = 0 + (𝜋/2) x = 𝜋/2 y = 3 sin (𝜋/2) y = 3 |
|
x = (𝜋/2) + (𝜋/2) x = 𝜋 y = 3 sin (𝜋) y = 0 |
x = 𝜋 + (𝜋/2) x = 3𝜋/2 y = 3 sin (3𝜋/2) y = -3 |
|
x = (3𝜋/2) + (𝜋/2) x = 4𝜋/2 = 2𝜋 y = 3 sin (2𝜋) y = 0 |
So, the points are (0, 0), (𝜋/2, 3) (𝜋, 0) (3𝜋/2, -3) and (2𝜋, 0)
Problem 2 :
y = (1/3) sin x
Solution :
Comparing the given function with y = A sin Bx
y = (1/3) sin x
A = 1/3, B = 1
Finding amplitude :
Amplitude = 1/3
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= 2𝜋/4
= 𝜋/2
Calculating Inputs and Outputs :
|
x = 0 y = (1/3) sin 0 y = 0 |
x = 0 + (𝜋/2) x = 𝜋/2 y = (1/3) sin 𝜋/2 y = 1/3 |
|
x = (𝜋/2) + (𝜋/2) x = 𝜋 y = (1/3) sin (𝜋) y = 0 |
x = 𝜋 + (𝜋/2) x = 3𝜋/2 y = (1/3) sin (3𝜋/2) y = -(1/3) |
|
x = (3𝜋/2) + (𝜋/2) x = 4𝜋/2 = 2𝜋 y = (1/3) sin (2𝜋) y = 0 |
So, the points are (0, 0), (𝜋/2, 1/3) (𝜋, 0) (3𝜋/2, -1/3) and (2𝜋, 0)
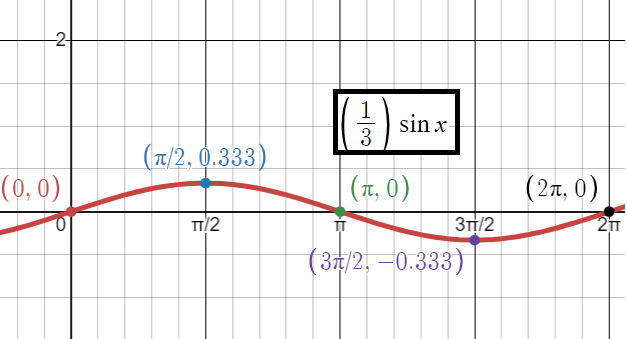
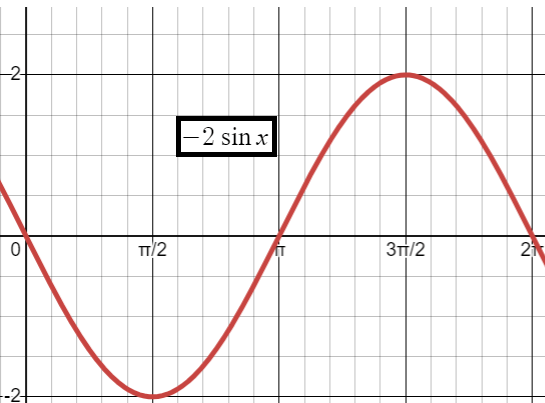
Problem 3 :
y = -2 sin x
Solution :
Comparing the given function with y = A sin Bx
y = -2 sin x
A = 2, B = 1
Finding amplitude :
Amplitude = 2
Since we have negative there should be reflection across y-axis.
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= 2𝜋/4
= 𝜋/2
Calculating Inputs and Outputs :
|
x = 0 y = -2 sin 0 y = 0 |
x = 0 + (𝜋/2) x = 𝜋/2 y = -2 sin 𝜋/2 y = -2 |
|
x = (𝜋/2) + (𝜋/2) x = 𝜋 y = -2 sin (𝜋) y = 0 |
x = 𝜋 + (𝜋/2) x = 3𝜋/2 y = -2 sin (3𝜋/2) y = 2 |
|
x = (3𝜋/2) + (𝜋/2) x = 4𝜋/2 = 2𝜋 y = -2 sin (2𝜋) y = 0 |
So, the points are (0, 0), (𝜋/2, 2) (𝜋, 0) (3𝜋/2, -2) and (2𝜋, 0)
Problem 4 :
y = sin (1/3)x
Solution :
Comparing the given function with y = A sin Bx
y = sin (1/3)x
A = 1, B = 1/3
Finding amplitude :
Amplitude = 1
Finding period :
Period = 2𝜋/|B|
= 2𝜋/(1/3)
= 6𝜋
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= 6𝜋/4
= 3𝜋/2
Calculating Inputs and Outputs :
|
x = 0 y = sin (1/3)(0) y = 0 |
x = 0 + (3𝜋/2) x = 3𝜋/2 y = sin (1/3 ⋅ 3𝜋/2) y = sin (𝜋/2) y = 1 |
|
x = (3𝜋/2) + (3𝜋/2) x = 3𝜋 y = sin (1/3 ⋅ 3𝜋) y = sin (𝜋) y = 0 |
x = 3𝜋 + (3𝜋/2) x = 9𝜋/2 y = sin (1/3 ⋅ 9𝜋/2) y = sin (3𝜋/2) y = -1 |
|
x = (9𝜋/2) + (3𝜋/2) x = 12𝜋/2 = 6𝜋 y = sin (1/3 ⋅ 6𝜋) y = sin (2𝜋) y = 0 |
So, the points are (0, 0), (3𝜋/2, 1) (3𝜋, 0) (9𝜋/2, -1) and (6𝜋, 0)
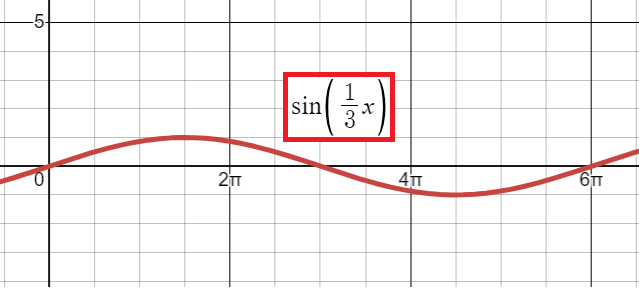
Problem 5 :
y = sin (x/2)
Solution :
Comparing the given function with y = A sin Bx
y = sin (x/2)
A = 1, B = 1/2
Finding amplitude :
Amplitude = 1
Finding period :
Period = 2𝜋/|B|
= 2𝜋/(1/2)
= 4𝜋
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= 4𝜋/4
= 𝜋
Calculating Inputs and Outputs :
|
x = 0 y = sin (0/2) y = 0 |
x = 0 + 𝜋 x = 𝜋 y = sin (𝜋/2) y = 1 |
|
x = 𝜋 + 𝜋 x = 2𝜋 y = sin (2𝜋/2) y = sin 𝜋 y = 0 |
x = 2𝜋 + 𝜋 x = 3𝜋 y = sin (3𝜋/2) y = -1 |
|
x = 3𝜋 + 𝜋 x = 4𝜋 y = sin (4𝜋/2) y = sin (2𝜋) y = 0 |
So, the points are (0, 0), (𝜋, 1) (2𝜋, 0) (3𝜋, -1) and (4𝜋, 0)
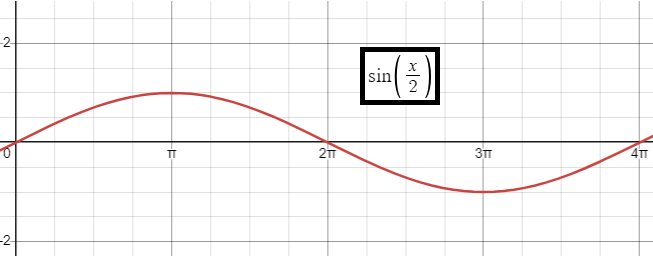
Problem 6 :
y = sin 3x
Solution :
Comparing the given function with y = A sin Bx
y = sin (3x)
A = 1, B = 3
Finding amplitude :
Amplitude = 1
Finding period :
Period = 2𝜋/|B|
= 2𝜋/3
Finding x-coordinates of key points :
Each input should add upto = Period / 4
= (2𝜋/3)/4
= 𝜋/6
Calculating Inputs and Outputs :
|
x = 0 y = sin (3(0)) y = 0 |
x = 0 + 𝜋/6 x = 𝜋/6 y = sin (3𝜋/6) y = sin (𝜋/2) y = 1 |
|
x = 𝜋/6 + 𝜋/6 x = 𝜋/3 y = sin (3𝜋/3) y = sin 𝜋 y = 0 |
x = 𝜋/3 + 𝜋/6 x = 3𝜋/6 = 𝜋/2 y = sin (3𝜋/2) y = -1 |
|
x = 𝜋/2 + 𝜋/6 x = 4𝜋/6 = 2𝜋/3 y = sin (3(2𝜋/3)) y = sin 2𝜋 y = 0 |
So, the points are (0, 0), (𝜋/6, 1) (𝜋/3, 0) (𝜋/2, -1) and (2𝜋/3, 0)
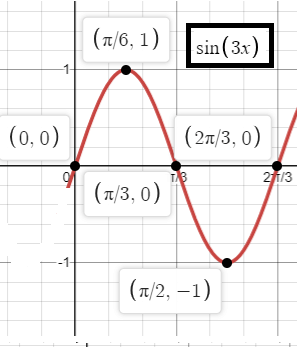
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling