SKETCH THE QUADRATIC FUNCTION WITH X INTERCEPTS

The graphical form of any quadratic function will be a parabola (the shape of U).

The quadratic equations which is in the form of

y = ax² + bx + c

may be open upward parabola or open downward parabola.

Based on the sign of leading coefficient, we may decide the parabola opens up or down.

How to find x-intercept ?

By applying y = 0, we can find the x-intercept.

If the quadratic equation is having two distinct real roots, the parabola will pass through those different points on the x-axis.

Graph crosses x-axis twice

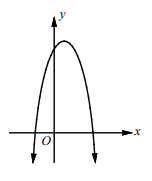
If the quadratic equation is having two same real roots, the parabola will intersect the x-axis once. (Multiplicity)

Graph crosses x-axis once

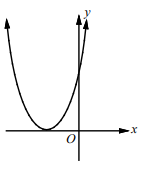
If the quadratic equation is having no real roots, the parabola will not intersect the x-axis.

Graph does not cross x-axis

Using axes intercepts only, sketch the graphs of:

Problem 1 :

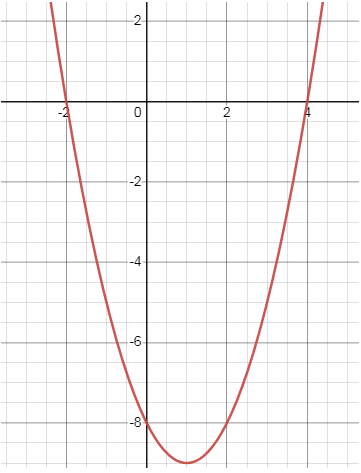
y = (x - 4) (x + 2)

Solution :

y = (x - 4) (x + 2)

Equating each factor to zero, we get

x - 4 = 0    x + 2 = 0

x = 4         x = -2

So, the parabola will cross the x-axis at -2 and 4.

y = (x - 4) (x + 2) ==> x² -2x - 8

Considering the coefficient of x², the sign is positive. So, the parabola opens up.

y-intercept :

When x = 0, y = -8

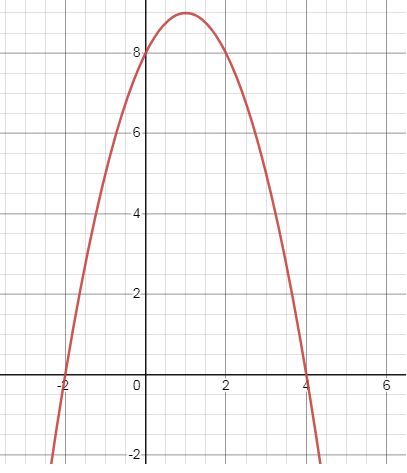
Problem 2 :

y = -(x - 4)(x + 2)

Solution :

y = -(x - 4) (x + 2)

Equating each factor to zero, we get

x - 4 = 0    x + 2 = 0

x = 4         x = -2

So, the parabola will cross the x-axis at -2 and 4.

y = -(x - 4) (x + 2) ==> -x² +2x + 8

Considering the coefficient of x², the sign is negative. So, the parabola opens down.

y-intercept :

When x = 0, y = 8

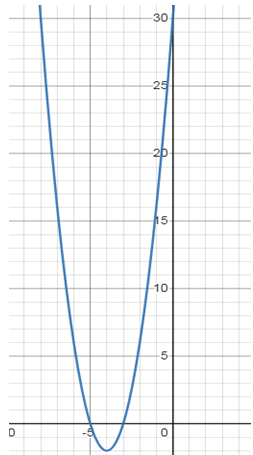
Problem 3 :    

y = 2(x + 3) (x + 5)

Solution :

y = 2(x + 3) (x + 5)

Equating each factor to zero, we get

x + 3 = 0    x + 5 = 0

x = -3         x = -5

So, the parabola will cross the x-axis at -3 and -5.

y = 2(x + 3) (x + 5) ==> 2x² +16x+30

Considering the coefficient of x², the sign is positive. So, the parabola opens up.

y-intercept :

When x = 0, y = 30

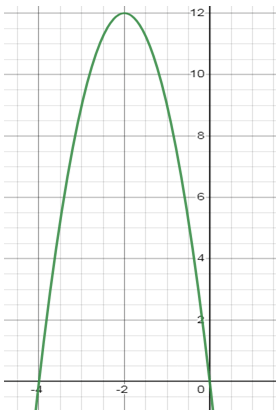
Problem 4 :

y = -3x(x + 4)

Solution :

y = -3x(x + 4)

Equating each factor to zero, we get

-3x = 0    x + 4 = 0

x = 0         x = -4

So, the parabola will cross the x-axis at 0 and -4

y = -3x(x + 4) ==> -3x² -12x

Considering the coefficient of x², the sign is negative. So, the parabola opens down.

y-intercept :

When x = 0, y = 0

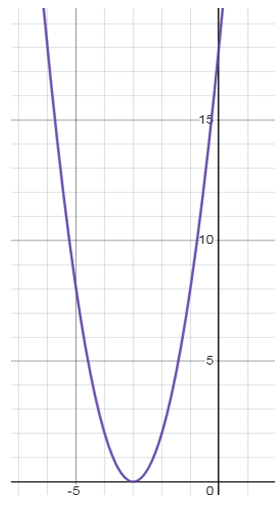
Problem 5 :

y = 2(x + 3)²

Solution :

y = 2(x + 3)²

Equating each factor to zero, we get

2(x + 3)² = 0

x = -3

So, the parabola will touch the x-axis at -3.

Considering the coefficient of x², the sign is positive. So, the parabola opens up.

y-intercept :

When x = 0, y = 18

Problem 6 :

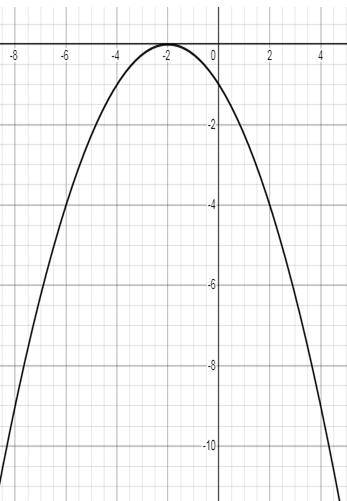
y = -1/4(x + 2)²

Solution :

y = -1/4(x + 2)²

Equating each factor to zero, we get

-1/4(x + 2)² = 0

x = -2

So, the parabola will touch the x-axis at -2.

Considering the coefficient of x², the sign is negative. So, the parabola opens down.

y-intercept :

When x = 0, y = -1